Веревочный многоугольник

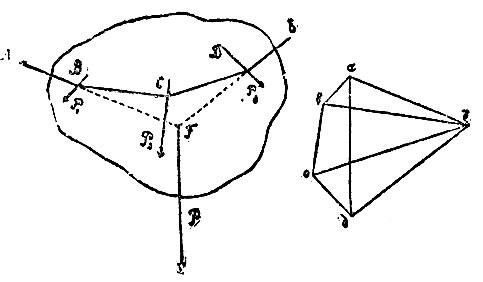
Веревочный многоугольник (иначе называемый нитяным) употребляется в графостатике вместе с силовым для графического (посредством одного чертежа, без вычислений) сложения или разложения сил параллельных и пересекающихся. Положим, дано сложить три силы: Р₁, Р₂ и Р₃, данные на чертеже. Строим сначала силовой многоуг. abcd, для чего проведем линию ab параллельно силе Р₁ и отложим на ней ab=P₁, затем далее bc || Р₂, cd || Р₃; тогда замыкающая сторона ad этого многоуг., называемого силовым, выразит равнодействующую наших сил по величине и направлению. Чтобы определить точку приложения равнодействующей на данном теле, поступаем так: берем произвольную точку e (полюс) и соединяем ее с вершинами силового м-а. Затем берем где-либо точку А и через нее проводим АВ || ae до пересечения с силой P₁, через В проводим ВС || be, через С проводим CD || ce и т. д. Получаем разомкнутый многоугольник, кот. и называется нитяным или В-ым, т. к. веревка приняла бы под действием наших сил как раз эту форму. Теперь, если продолжим линии АВ и DE до их взаимного пересечения в точке F, то через эту точку и пройдет наша равнодействующая, что и выражаем, откладывая Р II ad. Применение В-го м-а при сложных конструктивных расчетах значительно облегчает задачу, заменяя сложные вычисления сравнительно простым вычерчиванием.

Источники:

1. Энциклопедический словарь Русского библиографического института Гранат. Том 9/11-е стереотипное издание, до 33-го тома под редакцией проф. Ю. С. Гамбурова, проф. В. Я. Железнова, проф. М. М. Ковалевского, проф. С. А. Муромцева и проф. К. А. Тимирязева- Москва: Русский Библиографический Институт Гранат - 1924.