Волосность

Волосность, или капиллярность. Каждая частица жидкости находится под влиянием всех частиц, заключающихся в сфере молекулярного действия, в центре которого она сама находится. Между частицами тел твердых и жидких также приходится допустить существование взаимодействия или сил сцепления. Смотря по относительной величине, с одной стороны, сцепления между однородными частицами жидкости, с другой - сцепления между частицами твердого и жидкого тела, твердое тело иди смачивается, или не смачивается жидкостью. В первом случае жидкость пристает к поверхности твердого тела, на котором могут висеть капли жидкости и по поверхности которого капли жидкости расплываются. Поверхность жидкости, соприкасающаяся с твердым телом, оказывается около поверхности последнего несколько приподнятой (вогнутой), если твердое тело смачивается жидкостью, и несколько опущенной (выпуклой) - в противоположном случае. На рис. 1 MN - поверхность твердого тела, p - часть поверхности жидкости, смачивающей твердое тело. На частицу m, находящуюся около поверхности твердого тела, действуют сила сцепления со стороны частиц твердого тела, по направлению ms, и сила сцепления со стороны частиц жидкости по направлению mp, во внутрь самой жидкости. Допустим, что перевес на стороне первой силы, и что общая равнодействующая R (рис. 2. А) всех сил сцепления направлена во внутрь твердого тела. Поверхность жидкости всегда должна быть нормальна к силе, действующей на частицы, лежащие на этой поверхности, а потому касательная к поверхности жидкости в точке m должна в рассматриваемом случае иметь направление mT, чем и объясняется приподнятие или вогнутость поверхности жидкости. Когда перевес на стороне сил сцепления между однородными частиц. жидкости, то равнодействующая mR всех сил сцепления направлена во внутрь жидкости, как показано на рис. 2, В. В этом случ. касательная mT направлена вверх, чем и объясняется опускание или выпуклость жидкости около поверхности твердого тела. Угол в между внутренн. нормалями к поверхностям жидкого и твердого тел назыв. краевым углом (рис. 2). В первом случае (A) этот угол острый, во втором случае (B) он тупой. Если внутри трубки находится столб жидкости, то поверхности на его концах будут вогнуты, если жидкость смачивает материал трубки, и выпуклы, если она его не смачивает. Нормальное давление поверхностной пленки жидкости наибольшее, когда поверхность выпуклая, и наименьшее, когда поверхность вогнутая. На этом основаны явления капиллярности, или В. Если опустить трубку АВ (рис. 3) в жидкость, которая смачивает ее стенки, то нормальное давление на вогнутой поверхности mn, внутри трубки, будет меньше нормального давления на плоской внешней поверхности, вследствие чего жидкость в трубке поднимается до тех пор, пока давление приподнятого жидкого столба не будет равняться разности нормальных давлений внутри и вне трубки. Если же трубка погружена в жидкость, которая ее не смачивает, то жидкость внутри трубки имеет выпуклую поверхность, нормальное давление которой больше нормального давления вне трубки. Вследствие этого жидкость опустится настолько, что избыток давления сделается равным давлению жидкого столба, высота которого равна разности высот жидкости внутри и вне трубки (рис. 3 с правой стороны).

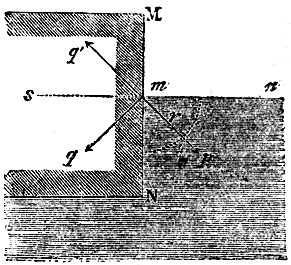
Рис. 1

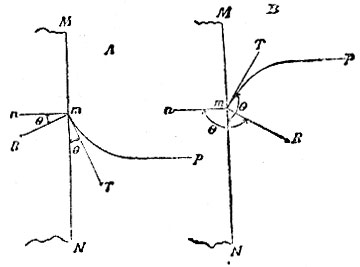
Рис. 2

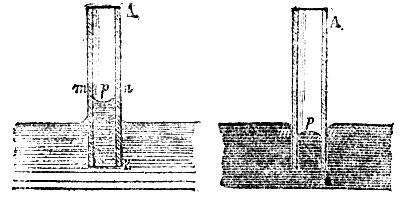
Рис. 3

Журен (Jurin, 1718 г.) дал закон, который, впрочем, еще раньше найден был Борелли: высота поднятия или опускания жидкости в волосной трубке обратно пропорциональна диаметру поперечного сечения канала трубки. Этот закон непосредственно вытекает из того, что краевой угол зависит только от жидкости и материала трубки, а не зависит от диаметра последней. Капиллярной постоянной называется величина, равная 2α:δ, где α - коэффициент, входящий в формулу Лапласа, для величины нормального давления у поверхности жидкости (см. жидкость), δ - плотность жидкости относительно воды. Капиллярн. постоянную обыкновенно обозначают через а². Высота h поднятия жидкости в капиллярной трубке равняется а²r, где r радиус поперечного сечения трубки в том случае, когда жидкость вполне смачивает материал трубки, т. е. когда краевой угол равен нулю. Вытекающая отсюда формула а²=hr может служить для определения капиллярной постоянной; если же смачивание неполное, то высота поднятия h=а²cosΘ:r, где Θ краевой угол. Если в жидкость опустить параллельно друг другу две вертикальные пластинки, то жидкость между ними также поднимается, при чем высота подъема в два раза меньше, чем в трубке, диаметр поперечного сечения которой равен расстоянию пластинок друг от друга. Этим явлением также можно воспользоваться для определения капиллярной постоянной. Если в жидкость опустить две пластинки, образующие малый двугранный угол (рис. 4), то жидкость поднимается тем выше, чем ближе она находится к ребру двугранного угла. Поверхность приподнятой жидкости пересекает стороны двугранного угла по кривым линиям - гиперболам. - На В. основано множество явлений всасывания жидкостей пористыми телами. Губка, сахар, пропускная бумага, мел, песок, дерево, литографский камень и т. д. с большой силой как бы втягивают в себя жидкость.

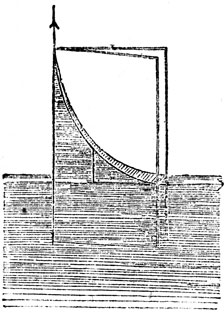
Рис. 4

Жамен (Jamin) построил различн. приборы, могущие служить для измерения этой силы. Явления В. играют также большую роль в растениях. Кроме упомянутых выше двух способов определения капиллярной постоянной, существует еще множество других. Если горизонтальную пластинку опустить до соприкосновения с поверхностью жидкости, то требуется некоторая сила для ее отрывания от жидкости. Измеряя эту силу, можно вычислить капилл. постоянную. Когда жидкость, наполняющая узкую вертикальную трубку, медленно выходит из ее нижнего конца, то образуются капли, которые спадают, достигнув определенного веса р. Перед отпаданием образуется между каплей и трубкой сужение, радиус горизонтального сечения которого r связан с весом р формулою р=2πrα, где α связано с капиллярн. постоянною а² формулой, указанной выше. Дюкло (Duclaux) устроил спиртомер в виде пипетки, емкость которой равна 5 куб. стм., с отверстием, из которого наполняющая ее жидкость вытекает по каплям. Число капель, получаемых при опоражнивании пипетки, указывает на процентное содержание чистого алкоголя, который определяется по готовой таблице. Чистая вода дает 100 капель, 90% спирт - 259 капель. Квинке (Quincke) пользовался методом капель для определения поверхностного натяжения α и капилл. постоянной а² расплавленных металлов. Капиллярная постоянная может быть далее определена путем измерения формы жидких капель, лежащих на поверхности твердого тела, ими не смачиваемого, а также путем измерения формы пузыря воздуха, находящегося внутри жидкости под горизонтальной поверхностью твердого тела. Поверхностное натяжение уменьшается с понижением температуры, как показали Бруннер, Вольф, Б. П. Вейнберг (в Петербурге) и др. При критической температуре жидкости (см. теплота) капиллярная постоянная равна нулю.

О. Хвольсон.

Источники:

1. Энциклопедический словарь Русского библиографического института Гранат. Том 11/Изд. 7.- Москва: Т-ва 'Бр. А. и И. Гранатъ и Ко' - 1911.