Высшая математика

Высшая математика. Это название принадлежит тем отделам математических знаний, которые стали развиваться с первой половины XVII века, благодаря идеям Декарта, Ньютона. Лейбница и целого ряда их великих последователей.

Математика вообще (и элементарная, и высшая) есть наука о величинах. Между величинами, которые мы встречаем как в теоретических соображениях, так и при изучении природы, мы различаем два различных класса: одни величины - постоянные, другие - переменные. Первые из них по существу дела проще вторых. Поэтому понятно, что внимание древних геометров было обращено на величины постоянные. Однако, как непосредственное наблюдение, так и изучение внешнего мира приводит нас к сознанию, что постоянных величин в природе очень мало, даже почти нет. Вокруг нас все непрерывно меняется, только с большею или меньшею скоростью: с течением дня меняется яркость солнечного света, меняется температура и давление атмосферы, земля непрерывно движется около солнца и вместе с солнцем участвует в более сложном мировом движении; едва ли во всей вселенной найдется одна неподвижная материальная точка. Эти изменения переменных величин происходит не случайно; они связаны между собою определенными законами. Меняя одну из величин, мы замечаем, что при этом и некоторые другие связанные с нею величины меняются, подчиняясь каждый раз одному и тому же определенному правилу. Так, сжимая газ под поршнем воздушного насоса, меняем его давление и температуру; нагревая металлический стержень, меняем его длину; вводя новое сопротивление в гальваническую цепь, меняем силу тока и т. д. Переменная величина, которая меняется по определенному закону при изменении другой, называется функцией этой другой величины, а эта последняя называется аргументом, или независимым переменным функции. В приведенных выше примерах давление газа мы назовем функцией его объема; длину данного металлического стержня назовем функцией его температуры, и т. д. Функция может зависеть от одного или нескольких аргументов: напр., давление данного количества газа есть функция объема и температуры; сила тока есть функция электродвижущей силы и сопротивления и т. д. Понятие о функции есть основное понятие, присутствие которого составляет отличительную черту В. м. от элементарной. Это уясняет одну из причин, почему древние так мало подвинули вперед изучение природы: им было чуждо понятие о функции; их математические методы давали возможность решать простейшие вопросы о площадях, объемах, о свойствах некоторых лишний, о равновесии тел. Для того, чтобы создать теорию движения и тех изменений, которые происходит в природе, нужны были новые понятия и связанные с ними методы. В. м. стремится выразить функциональную зависимость между переменными величинами помощью формул, изучить свойства этих функций помощью особых методов, составляющих содержание так называемого математического анализа, и уяснить их конкретно помощью наглядных геометрических образов. Преследуя свои отвлеченные теоретические цели, она в то же время дает натуралисту в руки сильное орудие для изучения природы, а технику позволяет овладеть этой природой и заставить ее служить для практических нужд человека. То широкое развитие техники, которым мы теперь пользуемся, есть результата приложения блестящих успехов, достигнутых в области математического анализа и естествознания два последние столетия.

Самое слово функция было введено в математику Лейбницем в 1692 г. Но понятие, соответствующее этому названию, вырабатывалось постепенно еще раньше, как это часто бывает в науке. Для полного уяснения нового понятия недоставало простого геометрического образа, который придал бы ему наглядность. Геометрия была доведена еще древними математиками до высокого совершенства; к началу XVII века уже значительно подвинулась вперед разработка алгебры. Но эти две науки не были между собою связаны общей идеей: геометрия того времени требовала большого напряжения воображения, алгебра была совершенно отвлеченною наукою. По словам Декарта, он задался мыслью исправить недостатки одной науки достоинствами другой. Это сближение геометрии с алгеброй было им осуществлено в 1637 году и послужило толчком к возникновению и быстрому развитию В. м. Новая наука, созданная Декартом, получила название аналитической геометрии.

Сущность метода аналитической геометрии заключается в том, что положение каждой точки на плоскости чертежа определяется помощью двух числовых величин, называемых координатами этой точки. Этой цели можно достигнуть различными способами, так что могут существовать разнообразные системы координата. Наибольшее применение имеет самая простая из этих систем, принадлежащая Декарту. Берем в плоскости чертежа две произвольные, но определенно выбранные пересекающиеся прямые Ox и Oy (черт. 1), называемые осями координата. Они разделять плоскость на 4 части, сходящиеся в точке пересечения осей O, называемой началом координат. Эти части плоскости называются по порядку: первая, вторая, третья, четвертая, как показано на черт. 1. Возьмем сначала точку M где-либо в 1-ой части плоскости. Проводим через нее прямую MN, параллельную оси у, до пересечения с осью x в точке N. Числовые величины отрезков ON и NM будут координатами точки M. Величина ON называется абсциссою, NM называется ординатою точки М. Первая из них обозначается буквою x, а вторая - y. Всякой точке первой части плоскости соответствует определенная пара положительных величин координат x и y. Обратно, каждой паре положительных чисел x, у соответствуем определенная точка 1-ой части плоскости. Для определения положения точек других частей плоскости условились ввести такое же правило знаков, как в тригонометрии при определении тригонометрических величин дуг различных четвертей окружности: отрезки оси x, откладываемые вправо от О считаются положительными, влево - отрицательными; отрезки, параллельные оси y, откладываемые вверх от оси x, считаются положительными, а вниз - отрицательными. Тогда всякая без исключения точка плоскости будет иметь определенную пару величин координат, и обратно, каждой паре величин координат будет соответствовать определенная точка плоскости. Если угол между осями x и y прямой, то координаты называются прямоугольными; в противном случае они косоугольные. Наибольшую простоту и применение имеют прямоугольные Декартовы координаты.

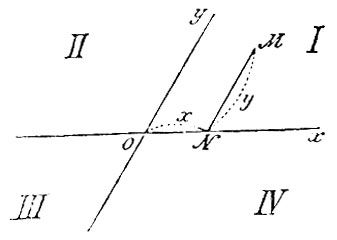
Черт. 1

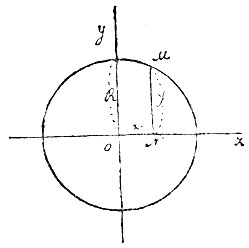
В математике, как элементарной, так и высшей, линия определяется как геометрическое место точек, построенных по некоторому закону, который дается в виде уравнения. Так, прямая есть геометрическое место точек, одинаково удаленных от двух данных точек; окружность есть геометрическое место точек, находящихся в равном расстоянии от центра; эллипс - геометрическое место точек, у которых сумма расстояний от двух данных точек, называемых фокусами, постоянна, и т д. В аналитической геометрии каждое такое равенство, определяющее геометрическое место, выразится в виде уравнения между координатами каждой точки данной линии. Так, в случае прямоугольных декартовых осей координат для прямой лиши мы получим уравнение 1-ой степени: y=ax+b (1), где b есть величина отрезка. образуемого данною прямою АВ на оси у (черт. 2), а а есть tg угла α, образуемого прямою АВ с осью x. Это значит, что какую бы точку М на прямой АВ мы ни взяли, ее координаты удовлетворят уравнению (1). Обратно, всякая пара величин х и у, удовлетворяющих уравнению (1), определяем точку, лежащую на прямой АВ. В этом смысле говорят, что прямая АВ выражается уравнением (1). Так же точно окружность, с центром в O, радиуса R (черт. 3) выразится уравнением: x²+y²=R² (2). Эллипс, у которого фокусы F₁ и F₂ лежат на оси х в равном расстоянии от О, выразится уравнением: 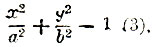при чем а и b суть величины отрезков, образуемых эллипсом на осях координат: они называются полуосями эллипса (черт. 4).

Черт. 2

Черт. 3

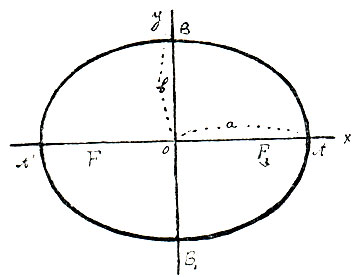
Черт. 4

Подобным же образом всякая линия на плоскости выразится уравнением, которому должны удовлетворять координаты каждой ее точки. Обратно, каждое уравнение между координатами выразит собою некоторую линию на плоскости. Решение всевозможных задач, касающихся линий на плоскости, сводится к исследованию и различным преобразованиям их уравнений. Так, желая найти точки пересечения двух данных линий на плоскости, мы должны найти такие величины х и у, которые удовлетворяли бы одновременно уравнениям обеих линий; а это значит, что мы должны решить систему двух уравнений с двумя неизвестными. Например, желая найти точки пересечения прямой (1) с окружностью (2), мы должны решить систему уравнений (1) и (2); из начальной алгебры известно, что такая задача сводится к решению одного квадратного уравнения.

Итак, способ координат приводить решение сложных геометрических задач к сравнительно более простым алгебраическим выкладкам. Он дает геометрам общие методы для решения задач, из которых почти каждая прежде требовала особого приема, большой изобретательности и напряженного воображения. Понятно, что со времен Декарта изложение геометрии значительно упростилось и наука быстро пошла вперед.

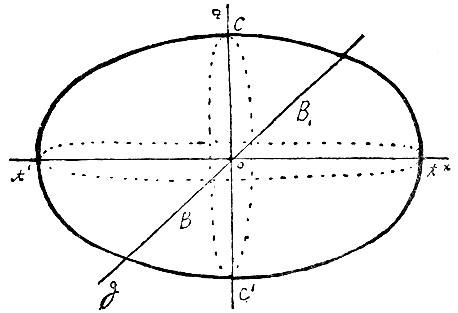
Систематическое изучение по методу координат свойств плоских кривых, выражаемых алгебраическими уравнениями, составляет содержание курсов аналитической геометрии на плоскости. Такие кривые называются алгебраическими кривыми и классифицируются по степени их уравнений в декартовых координатах. Линия, выражаемая уравнением первой степени, называется линией 1-го порядка и есть всегда прямая линия, как было упомянуто выше. Кривые 2-го порядка существуют трех видов: эллипс (к этому виду, как частный случай, принадлежит и окружность), гипербола и парабола. Форма уравнения в значительной степени зависит от положения кривой относительно осей координат. Поэтому стараются выбрать оси координат так, чтобы уравнение кривой было как можно проще. Выше мы видели, что при том выборе осей, который изображен на черт, 4, эллипс выражается уравнением (3). Точка О называется центром эллипса; относительно нее все точки кривой расположены попарно симметрично; всякая хорда, проходящая через центр, делится в нем пополам и называется диаметром эллипса; диаметры АА′ и ВВ′ называются главными осями: каждая из них делит эллипс на две равные и симметрично расположенные части.

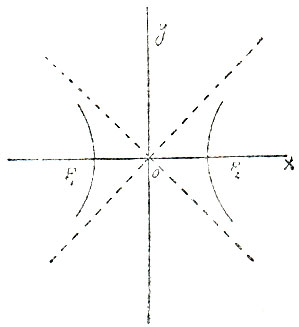
Гипербола есть кривая, все точки которой расположены так, что разность их расстояний от двух данных фокусов есть величина постоянная. Если выбрать оси координат подобным же образом, как для эллипса, то она выразится уравнением: 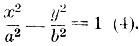Эта кривая состоит из двух отдельных ветвей (черт. 5) бесконечного протяжения; ветви, по мере удаления в бесконечность, приближаются к двум прямым линиям, изображенным на черт. 5 пунктиром и называемым асимптотами. Гипербола имеет центр и две главные оси, к которым асимптоты равно наклонены. Угол между асимптотами определяется величинами коэффициентов а и b уравнения (4). Если а=b, то асимптоты взаимно перпендикулярны, и гипербола называется тогда равностороннею. Приняв асимптоты за оси координат, мы представим уравнение гиперболы в еще более простом виде: ху=с (5). Равносторонняя гипербола в прямоугольных координатах выразится уравнением (5). Расположение ее относительно осей координат представлено на черт. 6.

Черт. 5

Черт. 6

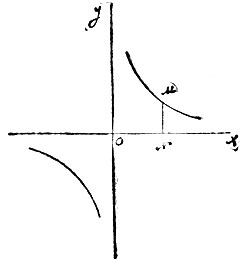
Парабола есть кривая, каждая точка которой равно отстоит от данного фокуса и от данной прямой, называемой директрисою. Если принять перпендикуляр FP (черт. 7), опущенный из фокуса F на директрису DD′ за ось х, средину О отрезка FP за начало координат, а перпендикуляр, восстановленный в этой точке к оси x, за ось у, то парабола выразится уравнением: у²=2рх (6). Парабола состоит из одной ветви бесконечного протяжения, асимптот она не имеет, не имеет и центра. Ось x служит для нее единственною главною осью. Характерное свойство параболы то, что касательная в какой угодно ее точке М равно наклонена к прямой MF, соединяющей эту точку с фокусом F, и к оси x. Этим свойством пользуются физики при устройстве параболического зеркала.

Черт. 7

Кривые 2-го порядка были найдены еще древними и изучались, как сечения прямого круглого конуса различными плоскостями. Поэтому они и до сих пор часто называются коническими сечениями. Аналитическая геометрия значительно облегчила изучение этих кривых.

Мысль распространить метод координат и применить его к геометрии в пространстве принадлежит самому Декарту. Она была осуществлена вскоре его последователями. Чтобы построить Декартовы координаты в пространстве, берут три произвольные, но определенным образом выбранные плоскости, пересекающиеся в одной точке и называемый плоскостями координат (черт. 8). Они разделять все пространство на 8 частей и пересекутся попарно по трем прямым, которые называются осями координат; осью x, осью у, осью z. Для определения положения какой-либо точки М, мы проводим через нее прямую параллельную оси z до пересечения с плоскостью xOe в точке N и из N ведем прямую NP, параллельную оси у, до пересечения с осью x в точке Р. Отрезок ОР обозначаем буквою x, отрезок PN - буквой у, отрезок NM - буквой z. Величины x, y, z суть координаты точки М. Для определения положения точки в какой угодно из 8 частей пространства вводится правило знаков подобно тому, как в геометрии на плоскости. Если оси координат попарно взаимно перпендикулярны, то они называются прямоугольными Декартовыми осями координат.

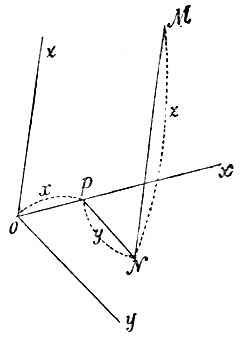
Черт. 8

Одно уравнение между координатами в пространстве выражает собою поверхность: всякая точка, координаты которой удовлетворяют этому уравнению, лежит на поверхности, им выражаемой. Если даны два уравнения между координатами точек пространства, то в отдельности они выразят собою две поверхности; совокупность же их выразит собою линию пересечения этих поверхностей. Поэтому линия в пространстве выражается системою двух уравнений.

Поверхности подразделяются по степени их уравнений в Декартовых координатах. Поверхность 1-го порядка есть всегда плоскость. Поверхности 2-го порядка, кроме конуса и цилиндра, бывают пяти различных видов: эллипсоид (изображенный на черт. 9), гиперболоид с одною полостью, гиперболоид с двумя полостями, эллиптический параболоид и гиперболический параболоид.

Черт. 9

Первые три из этих поверхностей имеют центр и по три главные плоскости, из которых каждая делит поверхность на две равные и симметрично расположенные части; последние две поверхности лишены центра и имеют только по две главные плоскости. Эллипсоид, гиперболоид с двумя полостями и эллиптический параболоид суть поверхности всюду выпуклые; гиперболоид с одною полостью и гиперболический параболоид суть поверхности седлообразные; характерная особенность этих двух поверхностей та, что на каждой из них прямая линия может уложиться на всем своем протяжении, и таких прямолинейных образующих на каждой из упомянутых двух поверхностей существуем бесконечное множество.

Курсы аналитической геометрии в пространстве посвящаются, главным образом, систематическому изложению свойств и решению задач на поверхности первых двух порядков и на прямую линию, при чем, понятно, прямая рассматривается как пересечение двух плоскостей и выражается поэтому системою двух уравнений первой степени.

Основное положение аналитической геометрии на плоскости: "линия выражается уравнением" позволяет, как видно из сказанного выше, исследовать свойства кривых помощью алгебры; то же положение позволяет графически изображать законы изменения функций. Если решить уравнение, выражающее кривую, относительно у, то в правой части равенства получится некоторая формула, содержащая в себе х; она выражает собою некоторую функцию аргумента x; следовательно, во всякой лиши ордината ее точки есть вполне определенная функция абсциссы. Мы находим выражение этой функции, решив уравнение относительно у. Поэтому говорят, что и в своем первоначальном виде уравнение определяем собою эту функцию, только в неявной форме. Простые примеры сказанного представляют приведенные выше уравнения: (1), (2), (5). Уравнение (1)представляется уже решенным относительно у; решив уравнение (2) относительно у, найдем: 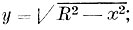уравнение (5) представится в виде: 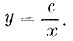Если нам дана какая-либо функция, имеющая теоретический интерес или выражающая некоторый закон природы, то мы строим ее величины в виде ординат для соответствующих значений аргумента; геометрическое место конечных точек построенных перпендикуляров будет кривая линия, изображающая наглядно течение данной функции. Когда построена такая кривая, то, рассматривая ее, измеряя ординаты различных ее точек и представляя себе точку, непрерывно бегущею по этой кривой, мы легко уясняем себе целый ряд особенностей функции: мы видим, при каких значениях аргумента функция положительна, и где она отрицательна; где функция увеличивается с возрастанием аргумента, и где убывает; где она достигаем наибольшего своего значения, и где наименьшего, и т. д. Хороший пример представляет приведенная выше равносторонняя гипербола xy=c (5), изображенная на черт. 6. Физика показывает, что, если изменять объем данного количества газа при постоянной температуре, то произведение объема на давление есть величина постоянная; если буквою x обозначить объем газа, а буквою у его давление, то уравнение (5) выразим собою упомянутый закон физики, а черт. 6 даст конкретное изображение этого закона. Так, из чертежа видно, что при малых значениях объема х давление у очень велико; при беспредельном увеличении объема x давление у падает, асимптотически приближаясь к нулю, но никогда его не достигая.

В настоящее время графический метод изображения функций применяется во многих науках: метеорологи строят кривые для изображения колебаний температуры и давления воздуха; статистики собранный ими числовой материал представляют в виде диаграмм; врачи составляют кривые температуры и веса больного для изображения хода болезни и т. д. Графический метод изображения функций, помимо указанной практической пользы, имел первостепенное значение в истории математики: он дал ключ к решению некоторых чисто теоретических задач, из которых развилось дифференциальное и интегральное исчисление. В изучении кривых линий геометрия издавна выдвинула два основных вопроса: 1) как провести касательную к данной кривой; 2) как вычислить площадь, ограниченную данной кривой. Эти задачи решались для простейших кривых искусственными приемами, основанными на частных свойствах отдельных кривых. При вычислении площади древние пользовались так называемым методом исчерпывания, но считали его недостаточно строгим и полученные помощью его результаты находили нужным проверить, подыскивая каждый раз доказательство от противного. Кавалиери в 1635 году предложил для той же цели новый метод неделимых, который был проще, но еще менее строг, чем древний метод исчерпывания. Декарт пользовался способом неопределенных коэффициентов, основанным на применении бесконечных рядов и довольно близко соприкасался с употребляемыми теперь приемами. Наконец, Ньютон предложил способ пределов. Основания этого способа теперь обыкновенно излагаются в курсах начальной геометрии, где он вытеснил прежний метод исчерпывания. Способ пределов находится в тесной связи с методом бесконечно малых: бесконечно малую величину можно определить, как разность между переменною величиной и ее пределом. Поэтому, как скоро установлено понятие о пределе, то тем самым установится и понятие о бесконечно малом, и обратно. Теория бесконечно малых представляет значительно больше удобств, чем способ пределов, укорачивая и упрощая рассуждения. Тем не менее прошло много времени прежде, чем она вошла во всеобщее употребление среди математиков. В настоящее время метод бесконечно-малых есть основной и характерный метод высшей математики. Дифференциальное и интегральное исчисления представляют собою систематическую разработку этого метода в применении к частному особенно важному случаю. Дифференциальное исчисление было предложено Лейбницем в 1684 году. Три года спустя появилось знаменитое сочинение Ньютона, где он излагал свой способ флюкций, достигавший той же цели, как и Лейбницево дифференциальное исчисление. Разница была в сущности в том, что Ньютон пользовался способом пределов, а Лейбниц ввел бесконечно-малые величины. Между великими учеными возник тяжкий спор о первенстве. Для нас теперь ясно, что оба они шли разными путями к одной и той же идее, которая смутно уже намечалась в трудах их предшественников.

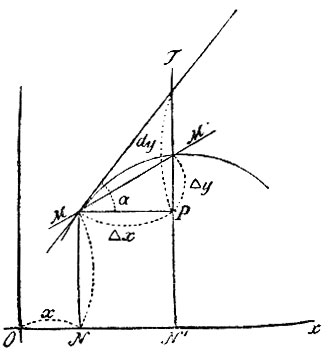
Уясним в коротких словах некоторые основные понятия и обозначения, встречающиеся в математическом анализе. Функцию аргумента х или, как обыкновенно говорят, независимого переменного х в общем виде обозначают символом ƒ (x); (буква ƒ есть первая буква слова fonction). Простейшие функции суть: 1) выражающиеся помощью конечного числа алгебраических действий, совершаемых над аргументом; они называются алгебраическими функциями; 2) показательная функция вида α^x, где α постоянная величина; 3) логарифмические функции; 4) функции тригонометрические; 5) функции обратные тригонометрическим, или так называемые круговые функции. Все эти функции называются элементарными, так как элементарная математика дает средства для исследования их свойств. Кроме них существует бесконечное множество других функций, более сложных. Какова бы ни была функция ƒ(x), уравнение у=ƒ (x) выразит некоторую линию. Если при бесконечно малом изменении величины аргумента х величина функции ƒ (x) изменяется бесконечно мало, то функция называется непрерывною функцией; кривая, изображающая течение такой функции, непрерывна в обыденном смысле этого слова. Анализ занимается исключительно непрерывными функциями. Построим кривую, выражаемую уравнением y=ƒ(x), возьмем на ней произвольную точку М с координатами х и у (черт. 10) и отметим на той же кривой точку М′, бесконечно близкую к М.

Черт. 10

Вследствие непрерывности функции ƒ (х) обе координаты точки М' будут бесконечно мало разниться от координат точки М. Бесконечно малые разности ON′-ON=NN′ и M′N′-MN=M′P называются приращениями координат и обозначаются символами Δx и Δy. Отношение этих приращений 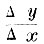равно tg угла наклонения прямой MM′ к оси x; и это справедливо, как бы близко М′ ни лежала к М. По мере уменьшения Δx, секущая прямая, поворачиваясь около точки M, приближается к положению касательной МТ к кривой в точке М. В пределе, когда Δ х обратится в нуль, секущая сольется с касательной, а отношение 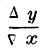сделается равным tg угла α наклонения касательной МТ к оси х. Итак, если кривая, выражаемая уравнением у=ƒ(x) имеем касательную, то отношение 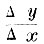имеет вполне определенный предел при Δх=0: этот предел равен tg α; он есть некоторая функция аргумента х, так как α меняется с изменением х по определенному закону, устанавливаемому видом кривой. Эта функция получила название производной функции ƒ(x) и обозначается символом f′(х). Так как огромное большинство кривых имеет касательную, то и большинство функций имеет производную. Дифференциальное исчисление дает общие приемы для нахождения производных. Они основаны на сравнительно небольшом числе формул и теорем и всегда приводят к цели, если производная существует. Производные элементарных функций оказываются функциями тоже элементарными. Примеры: производная от xⁿ есть nx^n-1 при всяком постоянном значении п; поэтому производная от самого аргумента х есть 1; производная от sinx есть cosx; производная от cosx есть - sinx, и т. д. В анализе во многих отношениях оказывается более удобным вводить в вычисления не самую величину производной, а только величину ей пропорциональную h.ƒ′ (х) где h есть множитель пропорциональности при ƒ′ (х); величина его совершенно произвольна, но не должна, однако, зависеть от х. Выражение h.ƒ′(x) называется дифференциалом от ƒ (х) или, что то же, дифференциалом от у; оно обозначается символом dy, так что dy = dƒ(x) - h.ƒ′(x). Выше мы видели, что производная от х равна 1; поэтому дифференциал независимого переменного х выражается так: dx=h. 1; он равен произвольной величине h. Разделив последние два равенства одно на другое, находим: 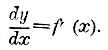Следовательно, производная равна отношению дифференциалов. В анализе ее обыкновенно представляют именно в виде dy/dx. Последнее равенство можно написать так: dy=ƒ(x) dx. Оно дает выражение дифференциала dy данной функции ƒ (х) через производную ƒ (x) от этой функции и дифференциал dx независимого переменного. Если, пользуясь произволом величины dx, положить ее равною приращению Δ х, то dy будет равно ƒ′ (х) Δ x, т. е. равно MP. tg α; из прямоугольного треугольника TMP следует, что тогда dy=TP; иными словами, дифференциал dy равен приращению TP ординаты точки касательной; он разнится от приращения М′Р ординаты точки кривой, на величину ТМ′. Этот геометрический смысл дифференциала может быть принять за его определение.

Так как производная ƒ′(x) есть тоже функция от х, то от нее можно по тем же правилам образовать новую производную, называемую второю производной от данной функции ƒ (х) и обозначаемую символом ƒ″(x). От ƒ″ (x) можно опять образовать производную - третью производную данной функции, обозначаемую символом ƒ″′ (х), и т. д. Функции ƒ″ (x), ƒ″′ (x),... называются производными высших порядков.

Правила дифференциального исчисления, позволяя находить производные от всевозможных функций, тем самым дают решение для упомянутой выше основной геометрической задачи о проведении касательной к кривой линии. С этою задачей в тесной связи находится целый ряд вопросов, касающихся свойств линий и функций. Так, довольно простые рассуждения показывают, что знак первой производной ƒ (х) характеризует возрастание и убывание функций: функция ƒ (х) возрастает вместе с величиной аргумента х там, где производная ƒ′ (х) положительна; она убывает с возрастанием величины аргумента х там, где производная ƒ (х) отрицательна. При тех значениях х, где имеет место равенство ƒ(х)=0, функция ƒ(x) достигает своего наибольшего или наименьшего значения. Этим пользуются для решения задач на maxima и minima, имеющих различные применения, научные и практические.

Введение производных высших порядков дало возможность еще глубже проникнуть в свойства кривых линий и функций. Этим способом исследуют направление выпуклости и вогнутости плоских кривых линий, их кривизну, особые точки (примеры таких точек представлены на черт. 11) и другие свойства. Одним словом, дифференциальное исчисление создало теорию кривых линий плоских и пространственных (не укладывающихся на плоскости), а также теорию кривых поверхностей. Эта теория в настоящее время стала выделяться в отдельную науку, называемую дифференциальной геометрией, которая, в свою очередь, выдвинула различные специальные вопросы. К числу их принадлежит изучение свойств линий на данной поверхности, так называемая геометрия на кривой поверхности, служащая обобщением планиметрии. Изучение линий на поверхностях с постоянной отрицательной кривизной привело Бельтрами к конкретному истолкованию геометрии без постулата Эвклида, созданной Лобачевским в средине XIX века.

Черт. 11

Одно из важнейших приложений дифференциального исчисления к изучению функций есть разложение их в бесконечные ряды. Рядом называется совокупность бесконечного числа членов, расположенных в определенном порядке. Если члены уменьшаются по числовой величине, по мере их удаления от начала ряда, то их сумма может оказаться конечною, хотя число слагаемых бесконечно велико. Примером может служить известная из начальной алгебры бесконечно нисходящая геометрическая прогрессия. Ряд, у которого сумма есть конечная и определенная величина, называется сходящимся. Признаки, позволяющие решать вопрос о том, сходится ли данный ряд или нет, называются признаками сходимости. Формулы Тайлора и Маклорена позволяют разлагать огромное большинство функций в сходящиеся ряды, расположенные по целым и положительным степеням аргумента. Так для sinx и cosx существуют следующие разложения:

справедливые при всяком конечном х. Ряды позволяют исследовать свойства функций, а также вычислять их величины и составлять таблицы для этих величин. Этим способом были составлены таблицы логарифмов, тригонометрических функций и др.

Отдельные исследования в области анализа были собраны, обработаны и приведены в стройную научную систему впервые Фйлером в XVIII веке. Он издал свои труды в трех обширных трактатах. Понятие о функции и связанные с ним методы анализа быстро нашли себе применение в области естествознания и техники. В механике длина пути, пройденного движущейся точкой за некоторый промежуток времени, есть функция длины этого промежутка, или, как говорят, есть функция времени. Первая производная от этой функции есть скорость движения точки, а вторая производная есть ускорение этого движения. Благодаря тесной связи механики с анализом создалась аналитическая механика, которая получила применение в физике, астрономии, а также в технических науках: инженерном деле, машиностроении, артиллерии и т. д.

Установив понятие о производной и разработав прием дифференцирования, Лейбниц поставил и обратную задачу: как по данному выражению производной найти первоначальную функцию, для которой данная служила бы производной. Иными словами, как найти функцию у, которая удовлетворяла бы уравнению 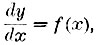, где ƒ(х) есть выражение данное? Эту искомую функцию Лейбниц назвал интегралом и обозначил так: 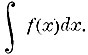Выражение ƒ (х) называется подинтегральная функция, а х - переменное интеграции. В противоположность производной, которая есть функция вполне определенная, интеграл содержит в своем выражении некоторый произвол: функций, удовлетворяющих уравнению 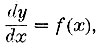существует бесконечное множество, но все они разнятся друг от друга только прибавкой некоторого постоянного слагаемого. Так, например, интеграл от x² представится в виде x³/3+c, где с есть какое угодно постоянное число. Различные выражения интеграла от х² будут разниться друг от друга только значениями постоянного слагаемого с. Вследствие присутствия в формуле интеграла произвольного постоянного слагаемого, интеграл получил название неопределенного интеграла. Мы видели выше, что производная от элементарной функции есть тоже функция элементарная и может быть всегда найдена по общим формулам дифференциального исчисления. Интегральное исчисление имеет иной характер: интеграл обыкновенно сложнее подъинтегральной функции по своим свойствам; очень часто интеграл довольно простой элементарной функции уже в элементарных функциях не выражается. Поэтому не может существовать и общих правил для нахождения интеграла, хотя мы и знаем, что интеграл существует. Первые главы курса интегрального исчисления посвящаются изучению тех классов элементарных функций, у которых интегралы выражаются в элементарных функциях, а также изложению различных приемов, позволяющих находить выражения интегралов в элементарных функциях, где такое выражение возможно.

Разработка интегрального исчисления обогатила науку еще большим числом открытий, чем дифференциальное исчисление, и расширило область математики во многих различных направлениях. Мы укажем только некоторые из них, наиболее резко выраженные.

I. Возьмем кривую, соответствующую уравнению у=ƒ(х) (черт. 12), проведем в ней две ординаты АА′ и ВВ′, соответствующие двум произвольно выбранным абсциссам OA′=а и ОВ′=b, лишь бы кривая в промежутке АВ была непрерывна. Вычислим разность между величиной интеграла 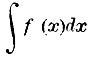при х=0 и ее величиной при х=α. Эту разность принято обозначать так: Так как при вычитании двух значений интеграла друг из друга произвольное постоянное сократится, то величина 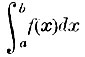будет вполне определенная; она называется поэтому определенным интегралом. Величины а и b называются его пределами. Ясно, что определенный интеграл не зависит от х. Величина его определяется только видом подъинтегральной функции ƒ(x) и величинами пределов. Если в выражение ƒ(x) или в выражения пределов входят какие-либо буквенные коэффициенты, то определенный интеграл будет функцией этих коэффициентов. Геометрический смысл определенного интеграла таков: он равен площади криволинейной фигуры А′АВВ′. Отсюда следует, что интегральное исчисление дает общий способ решить указанную выше основную задачу геометрии: вычислить площадь, ограниченную кривой линией. Всякий раз, когда такая площадь выражается в элементарных функциях, интегральное исчисление доводит решение задачи до конца.

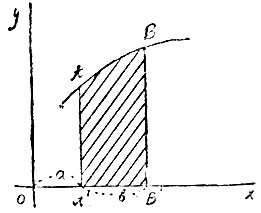
Черт. 12

Как только был решен вопрос о площади, ограниченной кривой, тотчас удалось найти выражения в определенных интегралах для длины дуги кривой лиши, для объема и поверхности тела, ограниченного кривыми поверхностями, а также в механике выражения для моментов инерции и координат центра тяжести различных тел.

II. Та особенность неопределенных интегралов, что они часто не могут быть выражены в элементарных функциях, дала новый толчок к дальнейшему развитию анализа. Такие интегралы стали изучать, как новые функции, разработали их свойства, составили для них таблицы, и они вошли в математику наравне с элементарными функциями, служа новым орудием для решения различных задач, которые прежде казались неразрешимыми. Так создалась теория эллиптических, ультраэллиптических, Абелевых и др. функций.

III. Определенные интегралы, как упомянуто выше, суть функции тех буквенных величин, которые входят в подъинтегральную функцию и в пределы. Если определенный интеграл не выражается в элементарных функциях, то он может быть изучаем, как новая функция сказанных буквенных величин, или, как говорят, параметров. Эта теория определенных интегралов особенно многим обязана Эйлеру. Функции, выражаемые в виде определенных интегралов, обладают своеобразными особенностями, совершенно чуждыми элементарным функциям. К числу таких функций принадлежат так называемые Эйлеровы интегралы.

Теория определенных интегралов нашла себе приложение в некоторых главах физики и механики, между прочим, в теории потенциала электрических и магнитных сил и притяжения материальных масс.

IV. Задача найти функцию у, удовлетворяющую уравнению 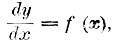есть частный случай более общей задачи: найти у из уравнения, в которое, кроме независимого переменного х, входит неизвестная функция у и ее производные различных порядков. Такие уравнения называются дифференциальными уравнениями. Функция, удовлетворяющая дифференциальному уравнению, называется его интегралом. Дифференциальные уравнения классифицируются по порядку старшей входящей в них производной от неизвестной функции. Так уравнение 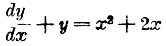есть дифференциальное уравнение 1-го порядка. Простой поверкой можно убедиться, что ему удовлетворяет выражение: у=х². Изучение различных видов дифференциальных уравнений, приемов их интегрирования и свойств интегралов уравнений, не интегрирующихся в элементарных функциях, составляет содержание теории дифференциальных уравнений.

К дифференциальным уравнениям приводится множество задач геометрии, механики и физики. Особенно широкое применение имеют дифференциальные уравнения в задачах, касающихся движения точек, тел твердых, жидких и газообразных, а также движения теплоты, электричества и т. д.

Большой интерес по своим последствиям имела постановка и решете задачи о колебании натянутой струны. Эта задача, так же как и все ей подобные, сводится к интегрированию некоторого дифференциального уравнения. Решил ее в общем виде впервые Даниил Бернулли в XVIII веке. Он представил ординату произвольно взятой точки струны как функцию абсциссы для любого момента времени, выразив эту функцию в виде бесконечного ряда, расположенного по синусам величин, кратных одной и той же дуги. Такие ряды получили название тригонометрических рядов. Из рассмотрения решения Бернулли оказалось, что при помощи тригонометрического ряда может быть в известных пределах выражена уравнением всякая кривая, хотя бы она состояла из отдельных кусков геометрических кривых (отрезков прямых, окружностей, эллипсов и т. д.) или даже просто без всякого правила начерчена от руки. С первого взгляда этот результат показался парадоксальным; он вызвал возражения со стороны ученых XVIII века против решения Бернулли и горячий спор между ними. Этот спор выяснил, что решение, найденное Бернулли, было верно, и в то же время оказал еще и другую пользу науке. Он привел к более правильному определению функций и к новой их классификации. Те функции, которые способны разлагаться в ряд Тайлора, получили название аналитических функций; остальные функции - неаналитических. Всякая аналитическая функция имеет как первую, так и всевозможные производные высших порядков. Между неаналитическими функциями есть такие, которые не имеют даже первой производной, хотя они при этом могут быть непрерывными. Литература, касающаяся таких функций, в последние десятилетия получила довольно широкое развитие и уяснила некоторые философские вопросы анализа.

Отдельную область математики, тесно связанную с теорией дифференциальных уравнений, составляет вариационное исчисление. Оно образовалось постепенно из отдельных задач на maxima и minima особого рода. Приведем из них несколько в виде примеров: 1) найти кривую, служащую кратчайшим путем между двумя точками на данной кривой поверхности (задача о геодезической лиши); 2) найти вид кривой линии между двумя данными точками пространства под условием, чтобы тяжелая материальная точка проходила ее в кратчайшее время (задача о брахистохроне); 3) найти вид тела вращения, встречающего наименьшее сопротивление при поступательном движении в жидкости по направлению оси вращения (задача Ньютона); 4) найти вид поверхности, проходящей через данный контур в пространстве и имеющей в пределах его наименьшую площадь и т. д. Основание вариационного исчисления относят к 1696 году, когда Иван Бернулли предложил упомянутую выше задачу о брахистохроне. Сначала задачи вариационного исчисления решались искусственными приемами на основании общих методов теории бесконечно-малых; значительные улучшения в этих приемах были сделаны Эйлером, но больше всего вариационное исчисление обязано Лагранжу, который построил его по такому же плану, как построено дифференциальное исчисление; он предложил для так называемой вариации новый символ δ, который по своему определению и свойствам очень близок к символу дифференциала. Приемы Лагранжа были впоследствии разработаны дальше и до настоящего времени лежат в основе курсов вариационного исчисления.

Характерную особенность математики XIX века составляет так называемая теория функций комплексного переменного. В алгебре давно уже чувствовалась необходимость наравне с действительными величинами ввести мнимое выражение √-1, которое обозначают обыкновенно символом i (от слова imaginaire). Комплексным количеством называется выражение вида: а+bi, где а и b суть величины действительные. Основное свойство комплексных количеств состоит в том, что какие бы алгебраические действия мы над ними ни совершали, в результате получится выражение того же вида, т. е. опять комплексное (действительное количество есть частный случай комплексного, когда b=0). Следовательно, комплексное число есть наиболее общий вид числа, к которому способна привести алгебра. Введение этих количеств в алгебру позволило получить для теорем формулировку самую простую и в то же время общую. В теории функций комплексного переменного самый аргумент функций есть величина комплексная. Эта теория была основана в начале XIX века Коши и получила быстрое и широкое развитие благодаря трудам самого Коши и его учеников, а затем Римана и целой школы немецких математиков, учеников и последователей Римана. Теория функций комплексного переменного дала сильное орудие для вычисления определенных интегралов, для выражения аналитических функций помощью различных видов бесконечных рядов и для исследования свойств этих функций; она уяснила многое прежде непонятное в свойствах функций, привела к открытию новых видов функций и совершенно преобразовала существовавшие ранее теории эллиптических, ультраэллиптических, Абелевых и друг. функций. Теория дифференциальных уравнений получила тоже новую обработку. Прежде усилия математиков в этой области были направлены, главным образом, к тому, чтобы найти выражения интегралов дифференциальных уравнений в элементарных функциях, где это возможно, или, по крайней мере, выразить эти интегралы помощью символа неопределенного интеграла. Количество задач, разрешимых этими способами, довольно ограничено. Теперь стали изучать интегралы дифференциальных уравнений, как функции переменных, входящих в уравнение, стремясь выразить их помощью бесконечных рядов и раскрыть их главные свойства. Через это в математике появились неизвестные ранее виды функций, к числу которых принадлежат гипергеометрические.

Во всех отделах математики, перечисленных в приведенном выше кратком очерке, всюду лежит в основе идея непрерывности: как аргумента, так и функция способны меняться непрерывно. По свойствам нашего ума мы легче представляем себе непрерывное изменение, чем изменение скачками. Мы почти не можем себе представить, чтобы точка перешла из одного положения в другое, не пройдя, хотя бы очень быстро, всю линию, соединяющую начальное положение точки с конечным. Поэтому мы стараемся объяснять все явления природы, исходя из идеи о непрерывности. Но далеко не все явления допускают такое объяснение; так, например, атомное строение материи, кристаллическая форма химических тел связана с числовыми законами неаналитическими. Соответствующая область математики в отличие от анализа называется теорией чисел, или аритмологией. Она по существу много сложнее анализа и потому менее его разработана. Однако, по своему значению она должна занять место рядом с анализом.

В теории чисел можно различать три главнейших отдела: 1) теория сравнений и теория квадратичных форм, рассматривающая различные вопросы в связи с решением неопределенных уравнений в целых числах, 2) теория прерывных или числовых функций, 3) теория алгебраических чисел. Основания теории прерывных функций были положены Эйлером в XVIII веке. Примеры таких функций представляют собою ρ (n) - число делителей целого числа n, ∫ (n) - сумма делителей целого числа n, φ (n) - функция, выражающая число чисел меньших n и с ним взаимно простых и т. д. Теория чисел изучает свойства и зависимость между числовыми функциями и отчасти применяет свои теоремы к теории рядов. Большое усовершенствование было внесено в эту теорию профессором Бугаевым, благодаря его учению о числовых производных, применению теории эллиптических функций и целому ряду работ по теории чисел. Числовая производная в теории чисел играет роль, сходную с обыкновенной производной в анализе. Теория алгебраических чисел изучает не только целые и рациональные числа, но и вообще числа, способные удовлетворять алгебраическим уравнениям. Она возникла из некоторых задач, выдвинутых высшей алгеброй, которая, вместе с исчислением конечных разностей, составляет как бы связующее звено между анализом и теорией чисел.

Исчисление конечных разностей имеет дело с конечным приращением функции (аналитической или числовой), соответствующим конечному приращению аргумента. Если обозначить приращение аргумента буквою h, то приращение функций ƒ (x) выразится так ƒ (x+h)-ƒ (x). Его обозначают символом Δ ƒ (х). В дифференциальном исчислении приращение h бесконечно мало, тогда и Δ ƒ (x) бесконечно мало, а предел отношения его к dƒ (х) есть 1. В исчислении конечных разностей h остается конечным, в большинстве задач h=l. Выражение Δ ƒ (х) называется конечною разностью. Теория конечных разностей дает формулы для нахождения Δ ƒ (х) по данной функции ƒ (х), а также решает обратную задачу: найти вид функции по данному выражению ее конечной разности. Эта функция называется интегралом по конечным разностям и обозначается так: 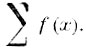. Отдел исчисления, занимающийся решением двух сказанных задач, очень напоминает собою соответствующие главы дифференциального и интегрального исчислений. Формулы этого отдела имеют применение к суммированию бесконечн. рядов, к приближенному вычислен. определенных интегралов и к интерполяции. Последняя задача имеет значение практическое. В опытных науках часто приходится производить непосредственное измерение величины функций при различных возможно близких между собою значениях аргумента; этот опытный материал можно расположить в таблицу или построить помощью его кривую, выражающую приблизительно течение наблюдаемой функций; задача интерполяции состоит в том, чтобы подобрать формулу, которая выражала бы как можно ближе построенную опытным путем кривую. Такие формулы носят название эмпирических формул. Они встречаются в физике, практической механике, инженерном искусстве и так далее.

Высшая алгебра есть дальнейшее развитие алгебры элементарной, от которой она отличается методами, заимствованными ею из других областей анализа, и большею трудностью решаемых ею задач. Алгебраисты средних веков дали формулы для решения уравнений первых 4-х степеней; но все их попытки решить подобными же приемами уравнения 5-ой и высших степеней не достигали цели. Тогда стали изучать зависимость между коэффициентами и корнями уравнения и свойства рациональных функций этих корней. Лагранж создал теорию симметрических функций, т. е. таких целых рациональных функций корней, которые не меняются при всевозможных перестановках этих корней между собой. Эти функции обладают тем свойством, что они всегда выражаются рационально через коэффициенты уравнения. Абель доказал невозможность решения в радикалах уравнения 5-ой и высших степеней в общем виде. После этого в высшей алгебре образовалось два течения. Первое из них занимается изучением тех классов уравнений, которые разрешаются в радикалах; второе имеет тесную связь с теорией функций комплексного переменного. Корень алгебраического уравнения изучается, как функция переменного, входящего в коэффициенты уравнения. Эта теория алгебраических функций почти неразрывно связана с теорией Абелевых функций. Кроме того оказалось, что теория алгебраических уравнений близко соприкасается и имеет большую аналогию с новой теорией дифференциальных уравнений, тем более, что алгебраические функции сами служат интегралами некоторых дифференциальных уравнений. Эта их особенность выдвинула вопрос о дифференциальных уравнениях с алгебраическими интегралами, которые, между прочим, нашли применение в механике, в задаче о движении твердого тела.

Литература по В. м. так обширна, что невозможно составить краткого перечисления хотя бы самых выдающихся сочинений. Весьма полезной справочной книгой по этой литературе может служить выходящая в последнее время "Encyklopädie der mathematischen Wissenschaften" (Leipzig). Много полезных сведений можно найти в курсах истории математики, между которыми видное место занимает Cantor, "Vorlesungen über die Geschichte der Mathematik" (Leipzig). См. также И. Тимченко, "Исторические сведения о развитии понятий и методов, лежащих в основании теории аналитических функций" и Д. Граве, "Энциклопедия математики" (1912).

Л. Лахтин.

Источники:

1. Энциклопедический словарь Русского библиографического института Гранат. Том 12/11-е стереотипное издание, до 33-го тома под редакцией проф. Ю. С. Гамбурова, проф. В. Я. Железнова, проф. М. М. Ковалевского, проф. С. А. Муромцева и проф. К. А. Тимирязева- Москва: Русский Библиографический Институт Гранат - 1933.