Счетные аппараты и пособия

Счетные аппараты и пособия.

Древнейшим счетным аппаратом является абак, или счетная доска. В древности абак служил единственным средством производства вычислений; он господствовал в Западной Европе до XVII века включительно. Наши счеты представляют собой разновидность абака. Устройство абака было чрезвычайно многообразно. В греческом абаке плоская поверхность так или иначе делилась на различные области; камешки, пуговки, шарики получали различное значение, смотря по тому, в какую область их клали; в римских абаках пользовались желобками и прутьями, как в наших счетах.

Нужно сказать, что счеты по сей день представляют собой не только простейшее, но и лучшее механическое приспособление для производства сложения и вычитания. Если для выполнения этих действий пользуются неизмеримо более сложными машинами, функционирующими при кассах, конторах и т. п., то это потому, что имеются в виду цели, совершенно чуждые арифметической стороне дела (контроль, автоматическое проставление итогов и т. д.). Усложнение аппарата действительно необходимо для выполнения более сложных действий - умножения, деления, комбинированных операций и т. д. Исторически, однако, первые счетные аппараты - и помимо абака - служили для выполнения сложения. По идее своей эти аппараты представляли соединение двух одинаковых скал, скользящих одна по другой. Если желаем, скажем, к 125 прибавить 316, то нужно поставить 0 второй скалы на 125 первой скалы и посмотреть, на какое деление первой скалы падает 316 второй. Чтобы такие аппараты были практичны, скалы должны иметь много делений; развитие этой идеи приводит к расчленению двух скал на несколько пар, - техника же дела сводится к возможному упрощению установки подвижных скал. Из этих приборов заслуживают упоминания аппараты Куммера (Kummer) и Болле (Bollée). Сюда же примыкают аппараты для умножения и деления, представляющие собой по существу подвижную таблицу умножения (аппараты Слонимского, Иоффе и друг.). Арифмограф Болле (фиг. 1) представляет собой первое органическое соединение аппаратов того и другого типа - переход к настоящей счетной машине.

Фиг. 1

Как мы уже сказали, главное назначение счетной машины есть не сложение (или вычитание), а умножение; но одни машины выполняют умножение, как повторное сложение, а другие делают это непосредственно; первые называются аддитивными, вторые - мультипликативными машинами.

Двум великим математикам принадлежит инициатива в этом отношении. Паскаль придумал первую настоящую машину для сложения, Лейбниц претворил ее в машину для умножения. Нужно сказать, что для Лейбница это был первый шаг к выполнению его грандиозной идеи - механизировать мышление.

С того времени счетная машина пережила сложную эволюцию. Первой представительницей современной счетной машины аддитивного типа нужно признать русский арифмограф Однера (фиг. 2); наиболее распространенная в настоящее время счетная машина "Brunsviga" представляет собой, по существу, переработку однеровской машины. Так как это типичная современная аддитивная машина, то на ней (фиг. 2) удобно выяснить конструкцию этих машин. Аппарат состоит из двух главных частей: барабана (SS) и каретки (LL). Барабан содержит внутри так называемый числительный аппарат, а каретка - передаточный аппарат. Барабан имеет ряд поперечных разрезов, вдоль которых проставлены цифры 1, 2, ... , 9. По разрезам движутся спицы или кнопки, которые движением руки устанавливаются на соответственных цифрах. Каретка состоит из двух частей: счетчика (QQ) и ответного ряда (ZZ). В последнем мы видим ряд отверстий, против каждого из кот. внутри каретки находится зубчатое "счетное" колесо с нанесенными на зубьях цифрами. Фиг. 3 изображает аппарат схематически: в барабане спицы поставлены на 12, а каретка на нуле. Под прорезом каждой спицы находится "движущее колесо"; все движущие колеса насажены на общую ось, которая поворачивается рукояткой К (фиг. 2). Фиг. 5 схематически изображает счетное колесо (меньшее) и движущее (большее). Зубья движущего колеса соединены с осью пружинами и зажаты пластинкой RR. Когда мы ставим спицу S на 1, пластинка сдвигается, и выскакивает один зуб; когда ставим спицу на 2, выскакивают 2 зуба движущего колеса и т. д. Если первая спица поставлена, как у нас, на 2, то при полном обороте рукоятки счетное колесо повернется выскочившими зубьями на 2 своих зуба, и вместо 0 в ответном ряду появится 2; при следующем обороте вместо 2 появится 4 и т. д. Если на барабане, как на рис. 3, поставлено 12, то в ответном ряду после первого оборота появится 12, после второго 24 и т. д. Счетчик с левой стороны каретки автоматически указывает число оборотов рукоятки. По этому плану, чтобы умножить число, скажем, на 235, нужно было повернуть рукоятку 235 раз; это слишком затруднительно. Именно для этого каретка и сделана подвижной: повернув рукоятку 5 раз, мы передвигаем каретку на один прорез вправо, так что аппарат получает расположение, изображенное на фиг. 4. Теперь для умножения на десятки множителя достаточно повернуть рукоятку 2 раза и т. д.

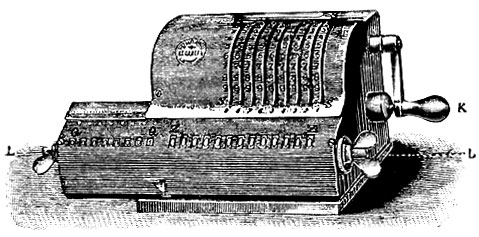
Фиг. 2

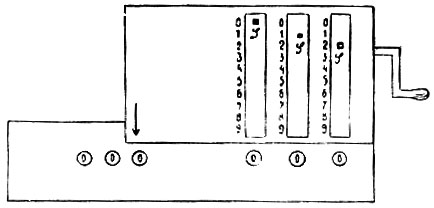
Фиг. 3

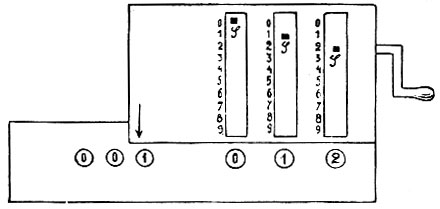
Фиг. 4

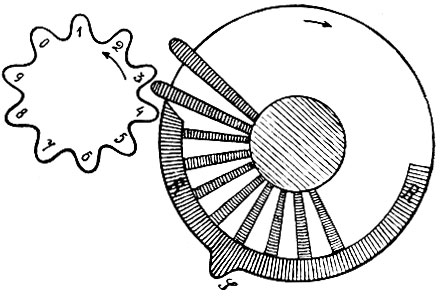
Фиг. 5

Самой трудной задачей в технике дела было наладить приспособление, которое передавало бы всякий раз в надлежащее место накопляющиеся единицы высших разрядов. Среди различных решений этой задачи очень видное место занимает схема, предложенная знаменитым русским математиком П. Л. Чебышевым. Мы лишены, однако, возможности описывать здесь эти приспособления подробно; заметим только, что наиболее обычны в этом отношении зубчатые передачи, наложенные так, что одно колесо делает 1 оборот на 10 оборотов другого.

Когда умножение выполнено, то на барабане отмечено множимое, на счетчике - множитель, в ответном ряду - произведение. Поэтому, если нужно произвести деление, то мы ставим делитель на барабане и вращаем рукоятку до тех пор, пока в ответном ряду не получим делимое или не превзойдем его; тогда на счетчике можно прочесть частное. Такова идея; действительное же выполнение несколько сложнее, так как вращение рукоятки необходимо комбинировать с передвижением каретки.

На совершенно ином принципе построены машины мультипликативного типа. Здесь основную часть аппарата составляет пластина, телесно представляющая табл. умножения (фиг. 6). Это Пифагорова таблица умножения, на каждой клетке которой поставлен стержень; длина стержня пропорциональна стоящей в этой клетке цифре. Аппарат приспособлен так, что всякий раз, как мы надлежащим образом установим на одном ребре пластины, скажем, стержень 3, а на другом - стержень 2, стержень, соответствующий произведению, нажмет рычаг таким образом, что он выбросит цифру 6. Комбинирование этого приема при многозначных производителях составляло наиболее трудную задачу в конструкции машин этого типа. Идея принадлежит Болле, наилучшее осуществление - Штейгеру (Steiger). Машины этого типа получили значительно меньшее распространение, чем аддитивные.

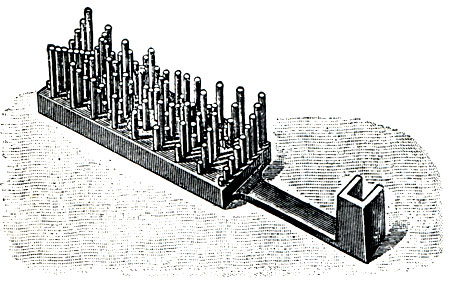
Фиг. 6

II Приближенные В. играют в практических применениях математики доминирующую роль. Причина этого заключается, с одной стороны, в том, что экспериментальные данные всегда имеют лишь приближенные значения, а с другой стороны, в том, что и теоретически иррациональные числа, к которым результаты сводятся в подавляющем большинстве случаев, могут быть выражены только приближенно. Погрешность, которою сопровождаются все такие В., обусловливается, таким образом, двоякой причиной: погрешностью исходных величин и погрешностью самого В., которое не может быть выполнено с полной точностью. Нужно сказать, что оценка погрешности или, вернее, пределов погрешности экспериментально полученных величин часто представляет весьма серьезные затруднения и производится обыкновенно на основании теории вероятностей (см.); но эта оценка относится уже к той дисциплине, в области которой произведены соответствующие измерения. К теории же приближенных В. относятся две задачи: какое влияние оказывают на результат погрешности исходных величин и, обратно, с какою точностью должны быть взяты исходные величины, чтобы мы могли быть гарантированы за определенную заранее точность результата. Сюда примыкает еще задача о том, какую погрешность дает В., остановленное на определенной ступени, если исходные данные известны в точности; и обратно, как далеко нужно вести В., чтобы быть гарантированным за определенную точность результата. Разность между истинным значением результата и тем, который мы получаем, останавливая его на определенной ступени, называется остатком, соответствующим этой ступени В-ия. Можно сказать без преувеличения, что наиболее характерной чертой математики XIX столетия является разыскание и исследование остатка, соответствующая каждому приближению. Почин в этом отношении принадлежит Лагранжу (1797, см. исчисление бесконечно малых).

Требуемая степень приближения выражается обыкновенно указанием единицы десятичного разряда, до которая точность должна быть доведена. Но если даны два числа с точностью до m-го десятичного разряда, то в их произведении мы можем гарантировать только m-2, а иногда даже только m-3 десятичных знака: так быстро падает точность с ходом В., если их не вести по строго определенному плану.

Непосредственное производство приближенных В. представляет собой прямое выполнение указаний теории. Но именно при приближенных В. это бывает особенно затруднительно, и потому здесь много пользуются различного рода вспомогательными средствами.

Табличное приближенное В. чрезвычайно распространено. Наибольшее (почти исключительное применение) имеют логарифмические таблицы (см. логарифмы). При применении логарифмических таблиц существенно важно определить, сколько знаков нужно брать в логарифмах при данных приближенных значениях чисел. Не так еще давно пользовались многозначными логарифмами там, где они совершенно бесполезны; напротив, иногда краткозначные логарифмы не достигают цели. Решение этого вопроса относится к теории логарифмов. Наиболее ценные 10-значные таблицы - это первые большие таблицы Флака (A. Vlack, "Arithmetica logarithmica"), первое издание которых появилось еще в 1628 году, и Вега (G. Vega, "Thesaurus logarithmorum", 1794, многократно переизданные); эти таблицы доведены до 100.000. Таблицы 9- и 8-значные не привились; зато 7-значные логарифмы долгое время применялись почти исключительно; из них наибольшим распространением пользуются таблицы Шрёна (L. Schrön) и Занга (Е. Sang). Из 6-значных таблиц наиболее известны Бремикера (С. Bremiker). Более краткозначные таблицы почти неисчислимы. Мы привели вообще лишь те, которые послужили типом и материалом для всех остальных таблиц.

Однако, в некоторых случаях необходимы логарифмы, вычисленные с гораздо большим числом десятичных знаков (напр., при вычислениях сложных процентов и срочных уплат за большие сроки). В. полных таблиц логарифмов с таким большим числом знаков сопряжено с большими затруднениями. Поэтому такие таблицы составлены для сравнительно ограниченного количества чисел, по которым уже вычисляются 20-значные логарифмы для всех чисел в известных пределах. Нужно сказать, что эти вспомогательные В. часто бывают довольно сложны; но к ним прибегают в тех случаях, когда непосредственное В. граничит с неосуществимостью. Таблицы Гоппе (Норре, "Tafeln zur 30-stelligen logarithmischen Rechnung", 1876) дают возможность вычислять даже 30-значные логарифмы.

Значение логарифмов заключается, главным образом, в том, что логарифм произведения очень просто определяется по данным логарифмам сомножителей. Леонелли (Z. Leonelli, 1802), а за ним Гаусс указали метод нахождения логарифма суммы по данным логарифмам слагаемых при помощи надлежащих таблиц. Эти приемы и таблицы в настоящее время значительно усовершенствованы. Но не нужно думать, что эти таблицы могут служить для облегчения сложения. Они применяются только для определения логарифма суммы, когда даны логарифмы слагаемых, а самые слагаемые не даны; таким образом, можно получить более точный результат, нежели путем предварительного определения слагаемых по их логарифмам.

Кроме логарифмических таблиц, при приближенных В. бывают полезны: 1) таблицы обращения простых дробей в десятичные (Oakes, Wucherer, Brocot и др.); 2) таблицы приближенных значений корней (Barlow, Jahn); 3) наконец, таблицы для решения уравнений; о последних несколько слов. Всякое уравнение 3-ей степени можно привести к виду x³±x=c. Таблица, содержащая сопоставление соответственных значений x и c, дает возможность решать всевозможные уравнения этого вида. Такого рода таблицу составил уже Ламберт (J. H. Lambert, 1770). Эту идею старались распространить на трехчленные уравнения более высоких степеней; но значительного развития она не получила.

Заканчивая вопрос о табличных В., мы должны обратить внимание на то, что в публике часто бывают распространены таблицы, не имеющие ни малейшего значения вследствие ошибочности и неправильности В. Пользуясь таблицами, нужно предварительно получить обстоятельные сведения об их научной ценности.

Связующее звено между табличным и графическим В. представляют так называемые графические таблицы. В простейшем виде графическая таблица строится следующим образом. Положим, что мы хотим построить таблицу значений функции logx; (при основ. 10). На вертикальной прямой в произвольном масштабе наносим с левой стороны обыкновенную скалу значений х. С правой стороны наносятся значения функции logx, но с таким расчетом, чтобы каждое из этих значений стояло против соответствующего значения аргумента х; следовательно, против 1 ставим справа 0, против 10 ставим 1, против 100 ставим 2 и т. д. Промежуточный деления справа наносим с тем же расчетом, т.-е., наприм., 0,5 ставим против того места левой скалы, которое отвечает значению √10, и т. д. Если скала достаточно густо нанесена, то значение логарифма читается непосредственно. По этому принципу строятся часто обширные таблицы. Никакая другая таблица по удобству отсчета и интерполяции не может сравниться с графической. Есть отрасли, в которых графические таблицы совершенно вытеснили всякие другие.

Собственно, графическое В. представляет собой непосредственное применение идеи Декарта в аналитической геометрии (см. высшая математика и геометрия). Если нам приходится вычислять значения функции y=ƒ(x), то мы стараемся начертить на основании геометрических соображений кривую, выражаемую этим уравнением; затем наносим данное значение x в качестве абсциссы и строим соответствующую ординату, длина которой выражает значение у. Удобство этого метода заключается в том, что он дает также возможность по данному значению у определить соответствующее значение (или значения) х. Затруднение заключается, конечно, только в вычерчивании кривой. Этот метод применяется поэтому обыкновенно в тех случаях, когда приходится постоянно вычислять значения одной и той же или нескольких определенных функций. Вычерченная кривая представляет собой как бы графическую таблицу значений этой функций. Дальнейшее развитие этой идеи представляет собой определение величин, связанных уравнением z=f(x, y). В этом случае каждому значению z отвечает некоторая кривая. Сообразно этому строится целая сеть кривых, соответствующих последовательным значениям z через известные интервалы; на каждой кривой у одного из ее концов отмечается соответствующее значение z. Желая с помощью этой "графики" определить значение z, отвечающее данным значениям х, y, мы строим точку х, y и смотрим, на какую кривую или вблизи какой кривой она падает. Ясно, что этим способом можно по значениям z и х определить y, а также по значениям z и y определить х. Мы имеем возможность выяснить здесь лишь простейшие приемы графического В. Нужно сказать, однако, что более сложные приемы и практически мало применимы и часто остаются лишь свидетельством остроумия их изобретателя.

Дисциплина, специально посвященная графическим методам выражения функциональной зависимости и вычисления, называется номографией.

Из аппаратов, служащих для приближенного В., наибольшее значение имеет так называемая логарифмическая линейка. Этот прибор состоит из двух скользящих друг по другу одинаковых скал, на которых деления нанесены пропорционально логарифмам отмеченных на них чисел (фиг. 7). Это значит, в начале скалы ставят не 0, как обыкновенно, а 1 (ее логарифм = 0); далее, 2 ставят на таком расстоянии, чтобы оно было равно lg2 в известных единицах; 3 ставят так, чтобы расстояние (1 3) было равно lg3 в тех же единицах и т. д. Чтобы при помощи логарифмической линейки помножить, скажем, 2,75 на 3,25, мы ставим начало второй скалы против деления 2,75 первой; так как сложение логарифмов соответствует перемножению чисел, то деление первой скалы, стоящее теперь против деления 3,25 второй скалы, выражает произведение. Этот прибор представляет для умножения, деления и возвышения в степень те же удобства, какие дают счеты для сложения и вычитания. Трудность изготовления счетной линейки заключается в необходимости большой точности при нанесении скалы; кроме того, на небольшом протяжении линейки трудно поместить значительную скалу. Отсюда - различные модификации в форме линейки, расположении скал, указателей и т. д. После счетов ни один аппарат не получил такого распространения, как логарифмическая линейка.

Фиг. 7

Числительные машины имеют для приближенных В. второстепенное значение. Относящиеся сюда приборы имеют в виду, главным образом, механическое решение уравнений. Собственно, принципы такой машины указаны, и именно - Вегаге (Wehage, 1877), Вильямом Томсоном (1878), Торресом (1895); но трудность заключается в многообразии коэффициентов и в их нанесении в каждом частном случае. Мы ограничимся тем, что приведем рисунок машины Торреса (фиг. 8).

Фиг. 8

Наконец, для механического решения уравнений предложено не мало чисто физических методов: весовой метод Гранта (G. Grant, 1896), в котором коэффициенты отмечаются различной нагрузкой, гидростатический метод Демоне (Demonet), электрический метод Люка (Lucas). Однако, все эти приемы также служат больше славе изобретателя, чем нуждам калькулятора.

В. Каган.

Источники:

1. Энциклопедический словарь Русского библиографического института Гранат. Том 12/11-е стереотипное издание, до 33-го тома под редакцией проф. Ю. С. Гамбурова, проф. В. Я. Железнова, проф. М. М. Ковалевского, проф. С. А. Муромцева и проф. К. А. Тимирязева- Москва: Русский Библиографический Институт Гранат - 1933.