Газы

Газы, так называются тела, обладающие следующими свойствами: 1) они весьма мало сопротивляются внешней причине, стремящейся изменить их форму; 2) сравнительно мало сопротивляются внешней причине, стремящейся уменьшить их объем; 3) не находясь под влиянием внешних сил (напр., силы тяжести), они равномерно наполняют все пространство, ими занимаемое, производя на поверхность тел, ограничивающих это пространство, давление, которое измеряют килограммами на кв. метр поверхности; это давление называется упругостью Г.; 4) если они не действуют химически друг на друга, то они относятся друг к другу вполне индифферентно, т. е. они вполне смешиваются, каково бы ни было отношение масс газов, помещенных в одно и то же пространство; 5) они приблизительно следуют закону Бойля-Мариотта: упругость данного количества Г. при неизменной температуре меняется обратно пропорционально его объему; 6) они приблизительно следуют закону Гей-Люссака: объем v данного количества Г. при температуре t° и объем v₀ при 0° связаны равенством v=v₀(l+αt), где для всех 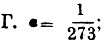7) они приблизительно следуют закону Авогадро: в одинаковых объемах различных Г. находящихся при одинаковых температуре и давлении, заключается одинаковое число молекул; 8) они приблизительно удовлетворяют условию отсутствия внутренней работы при изменении объема, или, иначе говоря, внутреннее сцепление между частицами весьма мало. В действительности Г. не удовлетворяют строго ни одному из последних 4-х свойств; замечаются отступления от этих законов, которые тем больше, чем ближе Г. находится к состоянию ожижения. Идеальным, или совершенным газом называется вещество, которое строго удовлетворяет приведенным четырем законам. В настоящее время удалось все без исключения Г. превратить в жидкое состояние: последним быль ожижен гелий Отсюда следует, что все Г. могут быть рассматриваемы как пары некоторых жидкостей, далекие от насыщения. Наоборот, пары жидкостей, далекие от насыщения, обладают всеми свойствами Г., так что разделение друг от друга понятий о Г. и о парах не может считаться обоснованным, если только не рассматривать пары в состоянии, близком к ожижению Наиболее правильным было бы сохранить название Г. для вещества, находящегося при температуре выше критической (см. теплота). когда оно ни при каком давлении не может перейти в жидкое состояние. Когда говорят о плотности паров, то всегда подразумевается, что пары находятся далеко от насыщения, т. е. обладают свойствами Г., а потому уместно рассмотреть сразу способ определения плотности Г. и паров. Следует отличать две плотности Г.: плотность D относительно воды, меняющуюся в весьма широких пределах при сгущении и разрежении Г., и плотность δ относительно воздуха, находящегося при одинаковых с Г. давлении и температуре. Вторая величина, почти постоянная для данного Г., была бы вполне постоянна, если бы рассматриваемые Г. и воздух одинаково или вовсе не отступали от законов Бойля-Мариотта и Гей-Люссака. По закону Авогадро следует, что вес одной молекулы различных Г. пропорционален плотности δ. При измерении молекулярного веса m принимают за единицу вес одного атома водорода, так что для водорода m=2. Молекулярный вес для других Г. равен m=28,88 δ. Для опытного определения плотностей δ и D существует целый ряд способов. Способ Реньо заключается в следующем: стеклянный шар, емкость которого около 10 метров, наполняется сухим Г.; при 0° и некотором давлении Н определяется его вес Р; затем при 0° Г. выкачивается до весьма малого давления h и вновь определяется вес р шара. Отсюда легко определить сперва вес Г., наполняющего шар при 0° и нормальном давлении 760 мм., а затем, зная объем шара, также и плотность D. Плотность δ найдется, если повторить те же измерения, наполняя шар сухим воздухом. При взвешивании шара необходимо вводить поправку на потерю веса в воздухе, которая зависит от давления, температуры и влажности воздуха. Чтобы избежать необходимости вводить эту поправку, весьма важную в виду малости определяемого веса P-p, Реньо уравновешивал шар А (рис. 1) другим шаром В, внешний объем которого с точностью равнялся внешнему объему шара А. Эти шары подвешивались под чашками весов в особых шкапах во избежание влияния на них потоков воздуха. Объем шара определялся взвешиванием шара, наполненного водою. Опыты Реньо дали для веса литра сухого воздуха при 0° и давлении 760 мм. в Париже 1,293187 гр. Позднейшие исследования Д. И. Менделеева показали, что этот вес равен 0,131844 д. гр. ±0,00010 гр., где g - ускорение силы тяжести, выраженное в метрах и зависящее от широты места и от высоты его над уровнем моря. Для Петербурга Д. И. Менделеев дает число 1,29455 гр. ± 0,00010 гр. Способ Гей-Люссака: в чугунный котелок (рис. 2), содержащий ртуть, погружена вертикальная, тщательно прокалиброванная трубка с и стеклянный цилиндр m, наполненный водою. Котелок установлен на небольшой печи; температура воды определяется термометрами t и t′. В пространство над ртутью вводится стеклянный запаянный пузырек а₀, содержаний известное весовое количество Р жидкости. При нагревании прибора пузырек лопается, и жидкость испаряется. Опыт непосредственно дает объем, температуру и упругость данного весового количества Г., откуда уже легко определяется его плотность. Гофман усовершенствовал этот способ, заменив воду, окружающую трубку с, парами какой-либо кипящей жидкости, выбираемой соответственно температуре, до которой желают нагреть испытуемые пары. Способ Дюма, подобно способу Реньо, основан на определении веса пара, объем, температура и упругость которого известны. В стеклянный шар В (рис. 3), снабженный вытянутой трубкой, помещают некоторое количество той жидкости, плотность паров которой желают определить. Шар продолжительное время удерживают при температуре, которая значительно выше температуры кипения жидкости при обыкновенном атмосферном давлении. Для этого иногда достаточно опустить шар в сосуд с водою, которую доводить до кипения (см. рис., на котором t представляет так называемый весовой термометр). Струя пара выходить из отверстия трубки. Когда выделение пара прекращается, запаивают кончик трубки и определяют для этого момента барометрическое давление, равное упругости пара, температура и объем которого также известны. Способ Виктора Майера (способ вытеснения) основан на идее, которая принадлежит Дюлонгу. Длинный, внизу расширенный, сосуд А (рис. 4) помещается в парах какой-либо кипящей жидкости, которую выбирают соответственно температуре кипения испытуемого вещества. Для этого могут служить: вода (100°), ксилол (140°), анилин (185°), дифениламин (310 м) и т. д. Температуру кипения этой жидкости, налитой в В, знать не нужно. Сосуд А соединен при помощи тонкой трубки с калибрированной трубкой g, в которой находится вода; она соединена с сосудом n, который легко поднимать и опускать, так что уровень воды в g и n можно удерживать одинаковым. В верхней части сосуда А находится отверстие, закрытое пробкой, и, кроме того, иногда приспособление, при помощи которого можно заставить в данный момент упасть на дно сосуда маленький шарик, содержащий известное весовое количество испытуемого вещества. Шарик упирается, напр., на палочку t, которую снаружи можно вытянуть настолько, чтобы шарик упал на дно сосуда А, покрытое асбестом. Сначала кипятят жидкость в В, пока выделение воздуха из сосуда А не прекратится, т. е, пока уровень воды в g не перестанет меняться. Затем вводят известное весовое количество испытуемого вещества в сосуд А, заставляя падать шарик или открывая на мгновение пробку. Быстро испаряясь, оно вытесняет некоторое количество воздуха, которое переходит в g; опуская сосуд n, удерживают уровень воды в g и n на одинаковой высоте. Пусть v объем воздуха, перешедшего в трубку g; t - комнатная температура и р давление воздуха в g. Допуская, что пары, образовавшиеся в А, настолько перегреты, что к ним приложимы законы Бойля-Мариотта и Гей-Люссака, мы заключаем, что эти пары при t° и давлении р занимали бы как раз объем v. Отсюда уже легко найти их плотность δ относительно воздуха. - Г. не следуют строго закону Мариотта. Произведение pv, упругости р на объем v при постоянной температуре, не есть величина постоянная для данного количества Г., но несколько меняется в зависимости от давления р. Если с увеличением давления р произведение уменьшается или увеличивается, то это значит, что объем v, получаемый при сжатии, соответственно слишком мал или слишком велик, т. е., что Г. сжимаются в первом случае более, во втором - менее, чем следует по закону Мариотта.

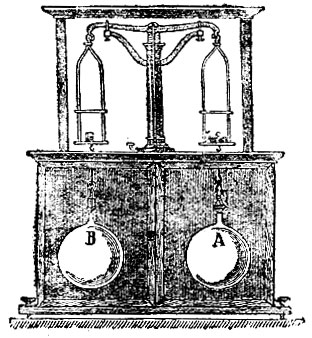
Рис. 1

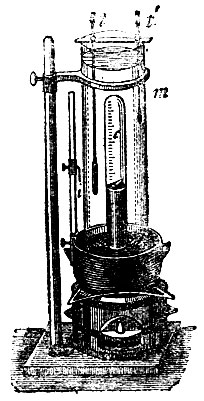
Рис. 2

Рис. 3

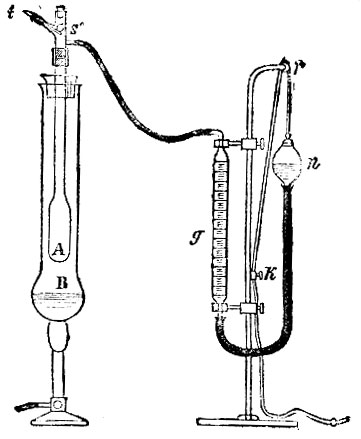
Рис. 4

Эрштедт и Свендзен (1826 г.) нашли отступления в сторону большей сжимаемости для Г., которые Фарадей в то время превратил в жидкое состояние (аммиак, сернистый газ и др.). Депрэ (1827 г.) доказал весьма простым опытом, что различные Г. сжимаются неодинаково и потому не все следуют закону Мариотта. Дальнейшие опыты производили Пулье, Дюлонг и Араго. Классические исследования произвел Реньо (1847-1862 гг.). Ему удалось избегнуть главного недостатка прежних опытов, который заключался в том, что, по мере увеличения давления, объем Г. непрерывно уменьшался, вследствие чего уменьшалась и относительная точность измерения этого объема. Реньо подвергал сжатиям тем большее количество Г., чем выше было достигнутое им давление, так что начальный объем v₀ Г. до дальнейшего его сжатия во всех опытах был один и тот же; самое же сжатие всегда доводилось до объема v=0,5v₀. Давление, которое до сжатия равнялось p₀, возросло бы до 2р₀, если бы газ следовал закону Мариотта. Измеряя новое давление р, Реньо мог открыть небольшие отступления от закона Мариотта. Реньо нашел, что воздух, азот и углекислый газ сжимаются больше, а водород меньше, чем следует по закону Мариотта. Зильестрем (1873 г., нашел, что при давлениях меньше 0,1 атмосферы водород сжимается более, чем следует по закону Мариотта; воздух же следует этому закону тем точнее, чем слабее давление. Д. И. Менделеев (1874-1876 гг.) пришел к совершенно другому результату, а именно, что в пределах давления от 5 мм. до 650 мм. воздух сжимается менее, чем по закону Мариотта. При давлении р>650 мм. воздух сжимается сильнее, чем следует по этому закону. Амага (1876-1883 гг.) пришел к мало вероятному результату, что воздух при слабых давлениях от 0,3 до 12,3 мм. строго следует закону Мариотта. Фукс (1888 г.) подтвердил результат Менделеева для воздуха. Для водорода он не нашел отступления от закона М. - Наттерер (1850-1854 гг.), Кальетэ (1870 г.) и Амага исследовали сжимаемость Г. при весьма больших давлениях; они нашли, что для т. наз. постоянных Г. (азот, кислород, водород и т. д.) сжимаемость при весьма сильных давлениях быстро уменьшается. Окись углерода, метан (болотный газ) и этилен (маслородный газ) при давлении выше одной атмосферы также сперва сжимаются более, а при весьма сильных давлениях - меньше, чем следует по закону М. Особенно замечателен этилен, который при некоторых давлениях сжимается в 2,2 раза больше, а при других (весьма высоких) в три раза менее, чем следует но закону М. Вроблевский нашел, что при весьма низких температурах водород сжимается больше, чем следует по закону М. Влияние температуры на сжимаемость Г. исследовали Реньо, Амага, Рот, Витковский и др. Все эти исследования показали, что при температуре, которая значительно выше критической, все Г. имеют свойство водорода, т. е. сжимаются менее, чем следует по закону М. Совокупность законов Мариотта и Гей-Люссака приводят к зависимости между объемом v, давлением р и температурой t данного количества Г., которая представляет уравнение состояния для Г.; оно иногда называется уравнением Клапейрона и имеет следующий видь: pv=RT, где T=t+273, абсолютная температура. Постоянная В пропорциональна взятому весовому количеству Г. и обратно пропорциональна его плотности 8. Если измерять v в куб. метрах, р в килограммах на кв. метр поверхности, то получается для одного килограмма газа R=29,27:δ. Если объем v измерять в куб. метрах, давление р в атмосферах и для каждого Г. брать грамм-молекулу, т. е. столько граммов, сколько единиц заключается в его молекулярном весе (2 гр. водорода, 32 гр. кислорода, 18 гр. водяных паров и т. д.), то для R получается одно и то же число для всех Г., а именно R=0,0815. Реально существующие Г. не следуют строго законам Мариотта и Гей-Люссака, а потому их уравнение состояния отличается от уравнения Клапейрона. Ван-дер-Вальс (1873) дал уравнение состояния для Г., имеющее следующий вид 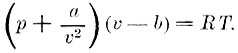В этом уравнении величина b равна четырехкратному объему, занимаемому молекулами Г.; величина а зависит от сцепления, существующего между молекулами Г. Клаузиус, Реньо и др. также предлагали различные формулы для уравнения состояния Г. - Теплоемкость Г. C при постоянном давлении и теплоемкость с при постоянном объеме связаны уравнением C-c=АR, где R постоянная формулы Клапейрона, А термический эквивалент работы, т. е. величина, обратная механическому эквиваленту тепла; для большой калории и килограмм-метра 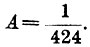Величина k=C:c равна 1,4 для кислорода, азота, водорода и воздуха. Эта величина входит в формулу для скорости звука (см.). Для углекислоты k=1,31; для одноатомных Г. k должно быть близко к 1,66, что и подтверждается для паров ртути; то же самое число найдено, напр., для аргона и гелия. Давление, производимое смесью Г., определяется законом Дальтона: давление смеси нескольких Г. равно сумме давлений ее составных частей, т. е. тех давлений, которые каждый из Г. обнаружил бы, если бы он один занимал объем. занимаемый смесью. Давления отдельных частей смеси называются парциальными давлениями. - Г. растворяются в жидкостях. Генри (1803) дал след. законы количество Г., растворимого при данной температуре в единице объема жидкости, пропорционально давлению Г., остающегося над жидкостью не растворенным. Вопросом о растворимости Г. занимались Бунзен и его ученики, далее Сеченов, Кумпф, Штейнер и др. Растворимость Г. уменьшается с повышением температуры. Наименьшею растворимостью в воде обладает гелий. Растворимость хлора в воде имеет максимум при 8°. Сеченов нашел, что растворимость Г. в воде, содержащей растворенные соли, меньше, чем в воде чистой. При сильных давлениях замечаются большие отступления от закона Генри для Г., хорошо растворимых. Объем жидкости при растворении в нем Г. увеличивается. Плотность раствора Г. в жидкости иногда больше, иногда меньше плотности самой жидкости. При растворении Г. в жидкостях иногда выделяется больше тепла, чем при их ожижении. Воздух, растворенный в воде, содержит 34% кислорода и 66% азота. Растворенные Г. выделяются из жидкости при уменьшении давления не растворенного Г., при повышении температуры, при затвердевании раствора, а также если в насыщенный раствор Г. ввести твердые тела с приставшими к ним слоями воздуха или иного Г. Это легко наблюдается, если в сельтерскую воду, переставшую выделять пузырьки, всыпать сахарный порошок, мелкие кусочки хлеба и т. п. Когда твердое тело соприкасается с газообразным, то могут обнаружиться два явления: сгущение Г. на поверхности твердого тела (адсорбция), которое особенно велико для тел пористых (абсорбция), и непосредственное поглощение Г. сплошною массою твердого тела (окклюзия). Соссюр (1814) исследовал абсорбцию различных Г. прокаленным углем букового дерева, морскою пенкой и гипсом. Уголь поглощает до 90 объемов аммиака, 35 объемов углекислого Г. и т. д. С возрастающей температурой быстро уменьшается сгущающая способность пористых тел. Губчатая прокаленная платина заключает в себе до 250 объемов кислорода, вследствие чего струя водорода, направленная в воздухе на губчатую платину, воспламеняется, на чем основано водородное огниво Деберейнера. Опыты Квинке, Жамена, Мозера и др. показали, что всякое твердое тело в соприкосновении с Г. покрывается очень тонким, но, вероятно, весьма уплотненным слоем этого Г. На этом основаны т. наз. изображения Мозера. Особенный интерес представляет поглощение водорода металлом палладием. Палладиевая проволока поглощает объем водорода, который при атмосферном давлении до 1.000 раз превышает объем самой проволоки. Н. Гезехус (в Петербурге) весьма тщательно исследовал поглощение водорода палладием и его сплавами с платиной, золотом и серебром. Между прочим, он измерял удлинение проволоки, сопровождающее поглощение водорода. Метеорное железо содержит до трех объемов Г., гл. обр. водорода. - Кинетическая теория Г., основанная Кренигом (1856 г.) и Клаузиусом (1857 г.), предполагает, что газовые молекулы, действующие друг на друга только при столкновениях, движутся, каждая, как вполне свободное тело, прямолинейно с некоторою скоростью. Направление движения резко меняется, когда молекула встречает стенку сосуда или молекулу того же или другого Г. Предполагается, что в обоих случаях перемена направления движения происходить согласно с законами удара упругих тел. Кроме прямолинейного движения, молекула может еще иметь вращательное движение. Кроме того, возможны еще и интрамолекулярные движения, т. е. движения атомов, составляющих молекулу, около некоторых средних положений. Такое представление о строении Г. объясняет их стремление равномерно занять предоставленный им объем, а также то давление, которое они производят на тела, с которыми соприкасаются. Это давление объясняется теми толчками, которые тела претерпевают от налетающих на них и отскакивающих молекул. Клаузиус показал, каким образом кинетическая теория Г. дает возможность вывести закон Мариотта. Основная формула имеет следующий вид: pv=¹/₃Nmu², где v объем газа, р его упругость, N число молекул, содержащихся в объеме v; m масса одной молекулы и u их скорость. Если живую силу поступательного движения газовых молекул обозначить через J, то можно написать pv=RT=²/₃J. Из этой формулы вытекает ряд следствий: энергия поступательного движения молекул Г. пропорциональна его абсолютной температуре. Скорость молекул данного Г. пропорциональна корню квадратному из абсолютной температуры; скорости молекул различных Г. при одинаковой температуре обратно пропорциональны корням квадратным из плотностей Г. При 0° скорость молекул равна для кислорода - 461 м., для водорода - 1843 м. в секунду. Для данного Г. энергия поступательного движения частиц составляет при всех температурах одну и ту же часть полного запаса энергии. Эта часть равна ³/₂(k-1), где k=C:c (см. выше). Максуэлль даль формулу, определяющую истинное распределение скоростей между молекулами Г., которые движутся, вообще говоря, с неодинаковыми скоростями. Из формулы Максуэлля вытекает, что средняя арифметическая всех скоростей молекул Г. составляет 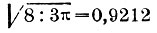от средней квадратичной скорости, т. е. от корня квадратного из среднего квадрата скорости. Средняя длина пути молекул Г., т. е. средний путь, пробегаемый ими между двумя столкновениями с другими молекулами того же Г., во столько раз больше одной четверти радиуса молекулы, во сколько раз объем, занимаемый Г., больше объема, действительно заполненного молекулами. Отсюда следует, что средняя длина пути обратно пропорциональна упругости Г. Средняя длина L пути молекулы и сумма Q площадей поперечных сечений всех молекул, содержащихся в единице объема Г., связаны удивительною формулою 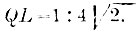. Внутреннее трение Г. не зависит от его плотности D т. е. оно одинаково как в сгущенном, так и в разреженном Г. Существует простая зависимость между внутренним трением (вязкостью) Г. и среднею длиною пути молекул. Вязкость Г. пропорциональна корню квадратному из абсолютной температуры. Средняя длина пути для молекулы кислорода при давлении в 760 мм. и температуре около 20° равна L = 0,000106 мм. В настоящее время существует целый ряд методов приблизительного определения размеров и числа молекул Г. Верхний предел для диаметра молекулы кислорода приблизительно одна миллионная мм. При 0° и 760 мм. находится в одном куб. стм. около двадцати трильонов молекул (20.10¹⁸). При адиабатическом изменении состояния Г., т. е. когда его объем меняется без теплового обмена с окружающими телами (весьма быстрое разрежение или сжатие), объем v, упругость р и абсолютная температура T связаны равенствами pv^к=Const. и Tv^к-1=Const., где k=C:c. Скорость истечения Г. из малого отверстия обратно пропорциональна корню квадратному из плотности δ Г., когда истечение происходит без изменения температуры. Бунзен построил основанный на этом прибор для сравнения плотностей Г. В Г. замечается явление диффузии (см.). Формула m=28,88 δ, связывающая молекулярный весь m и плотность δ Г. относительно воздуха, оказывается несправедливою для некоторых Г. и паров. Отступления объясняются распадением молекул на две или большее число частей; такое распадение молекул называется диссоциацией. Отношение числа разложенных молекул к числу всех молекул называется степенью диссоциации. Ее можно определить, если известна теоретическая плотность δ, истинная плотность и число составных частей, на которые распадается молекула. Степень диссоциации зависит при данной температуре от давления, под которым находится Г.

О. Хвольсон.

Источники:

1. Энциклопедический словарь Русского библиографического института Гранат. Том 12/11-е стереотипное издание, до 33-го тома под редакцией проф. Ю. С. Гамбурова, проф. В. Я. Железнова, проф. М. М. Ковалевского, проф. С. А. Муромцева и проф. К. А. Тимирязева- Москва: Русский Библиографический Институт Гранат - 1933.