Основные идеи геометрии

Основные идеи геометрии.

I. Содержание элементарной Г.

Классическая Г. сложилась еще в древности, и дальнейшее ее развитие заключалось, главным образом, в дополнениях второстепенного значения и в разработке связывающих материал логических концепций. Что касается самого материала, то содержание обычного курса элементарной Г. в средней школе мы предполагаем здесь известным. Мы здесь сделаем лишь сводку, которая дает возможность обозреть основные идеи и категории в связной концепции, а затем ознакомим читателя с основными задачами и идеями тех отделов, которые выходят из рамок строго элементарной Г.

1. В первую очередь, через всю Г. проходит классификация геометрических образов и выделение тех из них, которые, по своему значению в теории и приложениях, подлежат особому изучению. Первое подразделение заключается в классификации образов по числу измерений: они делятся на образы, не имеющие измерения (точки), образы одного измерения (линии), двух измерений (поверхности), трех измерений (тела). Однако, точное определение того, что, собственно, такое эти измерения, представляет большие затруднения. В аналитической и, во всяком случае, в метрической Г. (см. ниже) это нужно понимать так, что на образе одного измерения положение точки определяется одним данным (ее расстоянием от некоторой определенной точки), на двумерном образе - двумя данными (например, на плоскости ее расстояниями от двух неподвижных прямых), на трехмерном - тремя данными. Но, с одной стороны, чисто геометрического признака, свободного от всяких измерительных приемов, мы для этой цели не имеем; с другой стороны, в настоящее время придуманы, хотя и весьма искусственные, но все же вполне действительные способы определять положение точки на двумерном или трехмерном образе (например, на плоскости или в пространстве) одним заданием.

Из одномерных образов важнейшее значение имеет прямая. Определение прямой линии также представляет большие трудности, и большинство авторов относит это понятие к числу основных. С его помощью строится уже понятие об основном двумерном образе - плоскости. Вместе с тем все одномерные образы делятся на прямолинейные и криволинейные, все двумерные - на плоские и кривые. Учение об одномерных образах называли прежде лонгиметрией; нужно, однако, сказать, что классическая Г. таковой почти не знала, так как ни одна линия не изучалась независимо от поверхности, на которой она расположена. Учение о плоскости и образах, в ней расположенных, составляет планиметрию, учение об образах трехмерных - стереометрию. Важнейшие из планиметрических образов, помимо прямых, это углы и так называемые плоские фигуры, т. е. части плоскости, ограниченные со всех сторон линиями. В первую очередь, изучаются прямолинейные фигуры, т. е. фигуры, ограниченные прямыми линиями, и прежде всего простейшие из них - треугольники и четырехугольники. Из кривых линий преобладающее значение имеет окружность. "Начала" Евклида не рассматривают вовсе никаких других кривых линий; но классическая Г., как мы видели (XIII, 327), знала еще конические сечения и некоторые кривые другого вида, о которых скажем ниже.

Из образов трехмерных классическая Г. рассматривает двугранные и многогранные углы и так называемые геометрические тела, т. е. части пространства, ограниченные поверхностями со всех сторон. Важнейшие тела, которые изучает элементарная Г., это многогранники, т. е. тела, ограниченные плоскостями, и тела вращения, получающиеся путем вращения плоской фигуры вокруг неподвижной прямой (шар, цилиндр, конус). Такова в важнейших чертах общая классификация геометрических образов, принятая в классической и ныне в элементарной Г.

2. Расположение точек на геометрическом образе. На каждом образе, в первую очередь, устанавливаются действующие в нем нормы расположения точек. Относящийся сюда геометрический материал заключается в теоретическом обосновании понятий "между", "с одной стороны" и "с другой стороны", "внутри" и "вне". Древняя Г. оперировала всеми этими понятиями чисто интуитивно: но в настоящее время они устанавливаются и развиваются строго логически. Чтобы выяснить, в чем заключается содержание относящихся сюда рассуждений, остановимся на двух примерах. Во-первых, разберем деление плоскости прямою линией. Задача заключается здесь в том, чтобы установить следующее: если на плоскости дана прямая, то все остальные точки этой плоскости могут быть одним и только одним способом распределены в две категории таким образом, что прямолинейный отрезок, соединяющий две точки одной и той же категории, не встречает делящей прямой; всякий же отрезок, соединяющий две точки различных категорий, встречает эту прямую; эти две категории точек и составляют две стороны плоскости относительно прямой. Другой пример, деление плоскости замкнутой ломаной линией, заключается в следующем: все точки плоскости, этой ломаной не принадлежащие, распадаются на две категории; прямолинейные лучи, выходящие из точек первой категории и не проходящие через вершины ломаной, пересекают эту ломаную нечетное число раз; лучи, выходящие из точек второй категории, пересекают ломаную четное число раз; точки первой категории называются внутренними, точки второй категории - внешними; всякие две внутренние точки или две внешние могут быть соединены ломаной линией, не встречающей периферии; внутренняя же точка с внешней такой ломаной не может быть соединена.

Развитие учения о расположении точек геометрического образа заключается в установлении частных критериев, дающих возможность в отдельных случаях установить непосредственно, лежат ли те или иные точки внутри образа, на его периферии или вне его. Так, например, если мы соединим две точки, лежащие на разных сторонах угла, то все внутренние точки соединяющего отрезка лежат внутри угла; все же точки, лежащие на продолжениях этого отрезка, лежат вне угла. Если мы соединим две внутренние точки выпуклого многоугольника, то соединяющий их отрезок лежит целиком внутри многоугольника. Такого рода предложения совершенно необходимы, когда мы желаем действительно установить, где лежит та или иная точка; например, в каком случае центр описанной около многоугольника окружности лежит внутри многоугольника, на его периферии или вне его. Совокупность всех этого рода предложений составляет учение о расположении.

3. Учение об инцидентности. Сюда относится все то, что касается общих точек геометрических образов: условия, при которых точка лежит на данном образе, условия пересечения данных образов (прямых, прямых с кривыми, прямых с плоскостями и др. поверхностями и т. п.), определение числа общих точек и их расположения, условия касания линий и поверхностей, условия схождения нескольких линий в одной точке и нескольких поверхностей по одной линии. Существует обширная дисциплина, которая занимается только вопросами инцидентности; это - Analysis situs. Приведем примеры предложений элементарной Г., относящиеся к учению об инцидентности: прямая, имеющая с плоскостью две общие точки, лежит в ней целиком; две плоскости либо вовсе не имеют общих точек, либо имеют общую прямую; из каждой точки, лежащей в плоскости круга вне его, можно провести две касательные к окружности круга, и т. д.

4. Учение о геометрическом соответствии заключается в том, что каждой точке одного образа относят некоторую точку другого образа в качестве соответствующей ей. Выбор точки, соответствующей данной, можно осуществлять, конечно, многообразно; этим определяется характер соответствия. Элементарная Г. изучает, главным образом, двоякого рода соответствие: конгруэнтность и подобие. Конгруэнтность представляет собой такого рода соответствие двух образов, при котором они могут быть посредством движения приведены в совмещение таким образом, чтобы соответствующие точки совпали; в конгруэнтных образах расстояние двух точек всегда равно расстоянию соответствующих точек другого образа. Под подобием разумеют такое соответствие двух образов, при котором расстояние любых двух точек первого образа пропорционально расстоянию соответственных точек второго; иначе говоря, если А и В суть две точки одного образа, А′ и В′ соответствующие точки другого, то при подобии отношение АВ:А′В′ есть величина постоянная, т. е. не зависит от выбора точек А и В. Учение о конгруэнтности и подобии образов в элементарной Г заключается в установлении условий, при которых образы конгруэнтны или подобны, в разыскании соответствующих точек двух таких образов и в установлении между образами соотношений, проистекающих из их конгруэнтности или подобия. Конгруэнтность и подобие принадлежат, однако, к числу так называемых метрических соответствий, т. е таких, которые устанавливаются помощью понятий о равенстве и неравенстве, о численном значении отношения - вообще помощью понятия о величине. Существуют, однако, соответствия, которые устанавливаются чисто геометрическими методами, чуждыми всякой идее о величине. Приведем простой пример. Положим, что нам даны две плоскости Р и Р′ и некоторая точка О вне их. Пусть А будет произвольная точка первой плоскости; соединяя ее с точкой О, получаем прямую OA, которая пересекает вторую плоскость в некоторой точке А′; эту последнюю принимаем за соответствующую точке А первой плоскости. Таким путем каждой точке первой плоскости мы относим в качестве соответствующей ей некоторую точку второй плоскости; но это соответствие устанавливается чисто геометрически, без помощи понятия о величине, о равенстве и неравенстве; это соответствие неметрического характера. Метод, которым устанавливается это соответствие, называется центральной проекцией или, правильнее, проектированием из центра О, а самое соответствие двух плоскостей называется перспективным (см. отдел VIII).

Весь тот геометрический материал, который относится только к учению о расположении, об инцидентности, и о соответствии неметрического характера, составляет Г. положения в противоположность метрической Г.

5. Метрика играла в античной Г. второстепенную роль, но в современной элементарной Г. она имеет преобладающее значение. Под метрикой разумеют учение о геометрических образах с точки зрения их величины. Задача метрической Г. заключается, во-первых, в том, чтобы установить для каждой геометрической величины критерии сравнения, т. е. установить, при каких условиях мы считаем одно из двух значений величины равным другому, больше или меньше его, - а во-вторых, в измерены величины. Измерить величину значит выразить каждое значение этой величины числом, т. е. каждому значению величины отнести число; это должно быть сделано таким образом, чтобы конгруэнтным значениям ее были отнесены одинаковые числа, а значению, составленному из нескольких других ее значений, отвечало число, равное сумме чисел, отнесенных составляющим образам. Так, например, установить измерение площадей, значит выразить всякую площадь числом, т. е. каждой площади отнести число следующим образом: 1) конгруэнтным площадям должны быть отнесены одинаковые числа; 2) число, отнесенное площади, которая составлена из нескольких площадей, должно быть равно сумме чисел, отнесенных составляющим площадям. Чтобы этого достигнуть, оказывается необходимым и достаточным каждому значению величины отнести число, равное отношению этого значения к некоторому определенному условно выбранному значению той же величины (к единице меры). Вследствие этого, главная задача метрики в Г. заключается в следующем: a) в установлении критериев сравнения значений одной и той же величины; b) в определении отношения одного значения величины к любому другому значению той же величины; c) в выражении отношения более сложных величин через отношения более простых величин. Последний пункт играет особенно важную роль: некоторые авторы всю задачу метрики усматривают в том, чтобы заменить отношения площадей и объемов отношениями длин или комбинациями этих отношений. Чтобы найти, например, отношение площади треугольника к площади квадрата, достаточно найти отношения основания и высоты треугольника к стороне квадрата и взять половину произведения полученных таким образом чисел.

Классификация геометрических образов, учения о расположении, об инциденции, о соответствии и метрика - таковы категории, в которые укладывается все содержание элементарной Г. Содержание материала, входящего в состав этих категорий, мы считаем известным читателю настоящей статьи.

II. Конические сечения.

Кроме того материала, который в настоящее время "оставляет так называемую элементарную Г., в составе классической Г. входит учение о конических сечениях, составлявшее у древних венец и высшее достояние Г. Как греки пришли к этим замечательным кривым, мы в точности до сих пор не знаем. Прокл приписывает открытие их, как мы уже упомянули выше, Менэхму, ученику Платона, который пришел к ним при своих попытках решить знаменитую задачу об удвоении куба. Разыскание геометрических мест на плоскости, т. е. тех линий, на которых лежат точки, обладающие определенными свойствами, составляло одну из наиболее излюбленных задач греческих геометров. Такого рода задачи иногда ставились сами по себе, иногда возникали попутно, при решении задач на построение. В большинстве случаев геометрические места, которые разыскивали древние, сводились к прямой и к окружности; но более серьёзные задания приводили к более сложным кривым: из этих более сложных кривых самыми замечательными и в то же время наиболее простыми оказались конические сечения. Почему изучение этих кривых является естественным и прямым развитием материала элементарной Г., мы увидим ниже в отделе IV; здесь же мы заметим только, что каждый из последующих отделов как бы роковым образом с различных точек зрения приводит к этим замечательным трем кривым.

Итак, греки открыли конические сечения, как определенного рода геометрические места, независимо от конуса. Молодому современнику Менэхма-Аристею - приписывается открытие связи между этими геометрическими местами и конусом, т. е. определение этих кривых, как конических сечений. Основная идея здесь заключается в том, что при пересечении конических поверхностей плоскостью получаются кривые трех различных типов. Самые секущие плоскости геометры до Аполлония проводили всегда перпендикулярно к образующей конуса. Если конус остроугольный, т. е. имеет при вершине острый угол, то в сечении с плоскостью (как мы сказали, перпендикулярной к образующей) получается замкнутая кривая - эллипс (фиг. 1). Если конус тупоугольный, то сечение представляет собою разомкнутую фигуру (фиг. 2), ветви которой уходят в бесконечность; это - гипербола. Наконец, в прямоугольном конусе (т. е. с прямым углом при вершине) секущая плоскость, перпендикулярная к одной образующей, всегда оказывается параллельной некоторой другой образующей; сечение и в этом случае оказывается разомкнутой кривой, которая загибается, однако, гораздо медленнее, нежели гипербола (фиг. 3); эта кривая называется параболой.

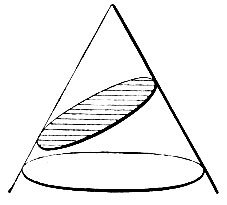
Фиг. 1

Фиг. 2

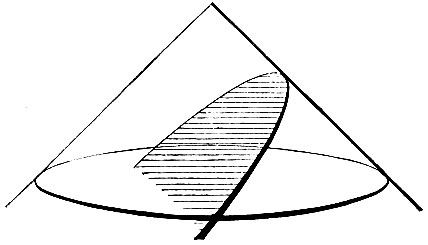
Фиг. 3

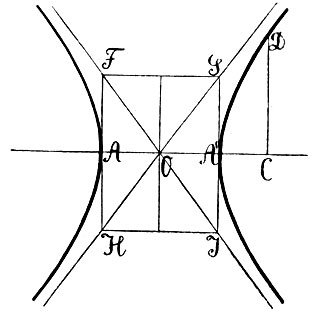
Однако, как мы сказали, греки не этим путем пришли к открытию конических сечений; они нашли их другим путем, как плоские геометрические места. До Аполлония наиболее обычный путь, которым определялись эти три кривые, заключался в следующем. Если мы возьмем окружность с диаметром АA′ (фиг. 4) и из произвольной точки С на диаметре восставим перпендикулярную к нему полухорду CD′, то последняя, как известно, представляет собой среднюю пропорциональную между отрезками диаметра, т. е. CD′²=АС. А′C; выражаясь языком древних, это значит, что квадрат, построенный на CD′ всегда равновелик прямоугольнику, построенному на отрезках AC и A′C. Можно поэтому сказать, что при данных точках A и A′ геометрическое место точек D′, для которых квадрат, построенный на CD, будет равновелик прямоугольнику AC×A′C, есть окружность.

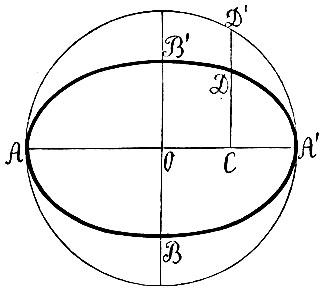
Фиг. 4

Если же мы теперь поставим себе задачей разыскать геометрическое место точек D, для которых квадрат, построенный на CD, будет не равен прямоугольнику АС×А′С, а будет составлять некоторую его часть, скажем n-ую, так что

(1),

то каждая точка D ляжет ближе к диаметру АА′, нежели D′, а геометрическое место точек D образует некоторую овальную кривую - эллипс. Центр окружности O называется также центром эллипса; диаметр АА′ называется большою осью эллипса (ее длину мы будем, согласно установившемуся обычаю, обозначать через 2а); перпендикулярный диаметр ВВ′ (2b) называется малой осью эллипса. Применяя соотношение (1) к отрезку ОВ′, будем иметь:

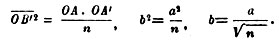
Для упрощения последнего соотношения положим n=m², так что соотношение (1) примет вид

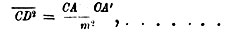
(2)

тогда b=a:m.

Если бы мы искали геометрическое место точек D таким образом, чтобы площадь квадрата CD² также сохраняла постоянное отношение к площади прямоугольника АС. А′С, но была бы больше этой последней, то мы также получили бы эллипс, только в нем диаметр АА′ был бы малой осью; соотношение (2) оставалось бы в силе, но число m было бы правильной дробью.

Положим теперь, что нам дан тог же отрезок АА′ (фиг. 5); взяв точку С не между А и А′, а на продолжении отрезка АА′, будем вновь искать геометрическое место точек D так. обр., чтобы площадь квадрата CD² составляла m²-ую часть площади прямоугольника АC. А′С, т. е., чтобы по-прежнему оставалось в силе соотношение (2). Теперь с удалением точки С расстояние CD будет постоянно возрастать, геометрическое место точек D составит разомкнутую линию - гиперболу; эта кривая состоит из двух симметричных веток, так как точку С мы можем брать по одну или по другую сторону отрезка. Здесь диаметр АА′(2а) называется действительною осью гиперболы, потому что он действительно пересекает кривую в двух точках А и А′. Перпендикулярная же к нему прямая ВВ′ кривой не пересекает; ее называют поэтому мнимою осью, и последней приписывают даже длину 2b, где, как и в случае эллипса, b=a:m.

Фиг. 5

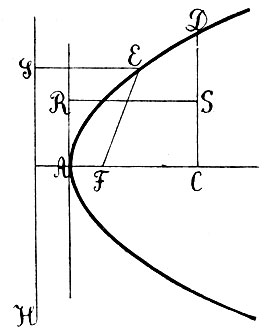
Эти древнейшие определения эллипса и гиперболы "по постоянному отношению площадей" аналогичны для обеих кривых. Для параболы полнота аналогии несколько нарушается. Здесь задача ставится так: на некоторой прямой АС (оси) (фиг. 6) будем выбирать произвольно точку С, а начальную точку А фиксируем; на перпендикуляре CD выберем точку D таким образом, чтобы квадрат, построенный на CD, был равновелик прямоугольнику, построенному на АС и на постоянном отрезке AR, т. е. чтобы

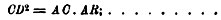
(3)

геометрическое место точек D представляет собой разомкнутую кривую - параболу. Этими определениями конических сечений пользуется, между прочим, Архимед, и их поэтому часто называют Архимедовыми определениями конических сечений. Доказать, что определяемые этими свойствами геометрические места совпадают с сечениями конуса, было трудной задачей, разрешение которой представляет один из перлов античной геометрии; вокруг этой задачи и сосредоточивалась теория, конических сечений древних. Евклид первый написал целый трактат о конических сечениях. Но подобно тому, как все руководства по элементарной геометрии стушевались и были забыты после появления "Начал" Евклида, так его собственное сочинение о конических сечениях потеряло значение после появления замечательного трактата Аполлония "О конических сечениях". Этот трактат имеет по отношению к этому высшему отделу классической геометрии то же значение, какое "Начала" Евклида имеют по отношению к элементарной геометрии.

Фиг. 6

Аполлоний начинает с нового определения конических сечений, действительно объединяющего все три кривые в одной общей идее: чтобы ее отчетливо выяснить, возвратимся к фиг. 6 и введем следующую простую терминологию. Исходную прямую АС будем называть осью. Из произвольной точки С этой оси был восстановлен перпендикуляр CD; квадрат, построенный на CD мы будем называть первым квадратом: квадрат, построенный на АС, вторым квадратом. Прямоугольник, построенный на АС и постоянном отрезке AR, мы будем называть вспомогательным прямоугольником. Тогда приведенное выше определение параболы сводится к следующему: парабола представляет собою геометрическое место точек D, выбранных таким образом, что площадь первого квадрата равна площади вспомогательного прямоугольника. Исходя из этой идеи, Аполлоний ищет геометрическое место точек D таким образом, чтобы площадь первого квадрата превышала площадь вспомогательного прямоугольника и при том на величину, пропорциональную площади второго квадрата; полученная таким образом кривая есть гипербола. Если же площадь первого квадрата меньше площади вспомогательного прямоугольника на величину, также пропорциональную второму квадрату, то соответствующая кривая будет эллипс. Это различие и выражается по-гречески самыми названиями кривых, также принадлежащими Аполлонию. Пользуясь современными обозначениями, мы можем сказать, что все конические сечения определяются условием:

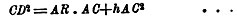
(4)

При положительном значении h кривая представляет собою гиперболу, при отрицательном - эллипс, а при h=0 - параболу. Задача Аполлония заключалась прежде всего в том, чтобы обнаружить тождество этих кривых с теми, которые соответствуют Архимедовым определениям, и с плоскими сечениями, конических сечений. Но здесь Аполлоний идет дальше - он показывает, что нет необходимости брать остроугольный, тупоугольный и прямоугольный конусы для получения трех кривых. Для этого достаточно только надлежащим образом выбирать наклон секущей плоскости к образующей конуса. Мы выясним это несколько иначе, чем это сделано у Аполлония, если представим себе (фиг. 7) круглый конус о двух полах, т. е. неограниченно продолженный в обе стороны. Если мы такую коническую поверхность рассечем плоскостью, встречающей только одну полу и непараллельной ни одной образующей, то мы получим в сечении замкнутую кривую - эллипс; этот эллипс обращается в круг, когда сечение перпендикулярно к оси. Когда плоскость становится параллельной одной из образующих, кривая размыкается, и мы получаем параболу. Наконец, когда плоскость наклонена к оси настолько, что она встречает уже обе полы, мы получаем две разомкнутые ветви, составляющие в совокупности гиперболу.

Фиг. 7

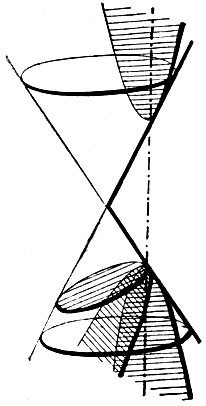
Если мы из вершины малой оси эллипса ВВ′ (фиг. 8) опишем окружность радиусом, равным большой полуоси, то эта окружность пересечет ось АА′ в двух точках F и F′, которые Кеплер позднее назвал фокусами (у Аполлония они носят громоздкое название). Из построения этих точек следует, что

Фиг. 8

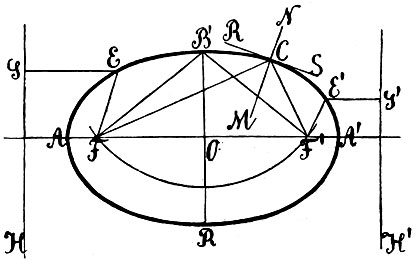
Это свойство принадлежит, однако, всякой точке эллипса; именно, для всякой точки С эллипса сумма ее расстояний от фокусов (FС+F′С) равняется большой оси (2а). Мало того, этим свойством эллипс вполне определяется: эллипс есть геометрическое место точек, сумма расстояний которых от двух неподвижных точек (фокусов) имеет постоянную величину. Такие же две точки есть в гиперболе; они расположены с внутренней стороны каждой ветки (фиг. 9) и обладают аналогичным свойством: разность расстояний каждой точки кривой от фокусов представляет собой постоянную величину, равную длине действительной оси гиперболы:

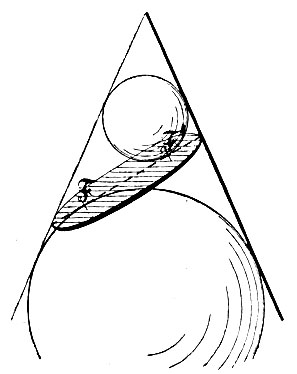
и здесь это свойство в таком же смысле может служить для определения кривой: гипербола представляет собой геометрическое место точек, разность расстояний которых от двух неподвижных точек есть величина постоянная. Французский математик Кетле (Quetelet, XIX ст.) показал, в какой связи стоят эти точки с сечениями конуса. Если мы впишем в коническую поверхность шар таким образом, чтобы он касался также секущей плоскости, то точкой касания будет служить фокус (фиг. 10). Если плоскость не параллельна образующей, то таких шаров будет два - им соответствуют два фокуса. Когда же плоскость параллельна образующей, то есть только один такой шар, - парабола имеет только один фокус.

Фиг. 9

Фиг. 10

Однако, приведенные выше фокальные свойства эллипса и гиперболы не распространяются на параболу. Но греческий геометр Папп, живший в III веке после P. X., указал другое замечательное свойство фокусов, легко распространяющееся также и на параболу. Именно, он показал, что каждому фокусу отвечает некоторая прямая, которую гораздо позже французский математик Делагир (De la Hire, XVII ст.) назвал направляющей, или директрисой этого фокуса. Все конические сечения обладают тем свойством, что отношение расстояний каждой точки кривой от фокуса и от директрисы есть величина постоянная.

Расположение директрис относительно фокусов видно на рис. 6, 8 и 9, где они отмечены через GH и G′H′. На всех кривых оказывается постоянным отношение EF:EG; но в случае гиперболы это отношение оказывается больше 1, в случае параболы оно равно 1, в случае эллипса оно меньше 1. Вместе с тем мы получаем следующее общее определение конического сечения: коническое сечение есть геометрическое место точек, для каждой из которых отношение ее расстояний от некоторой неподвижной точки (фокуса) и от неподвижной прямой (директрисы) есть величина постоянная. В эллипсе и гиперболе это отношение равно также отношению расстояния между фокусами к большой оси; это число Кеплер назвал эксцентриситетом конического сечения; таким образом, в эллипсе эксцентриситет представляет собою правильную, в гиперболе - неправильную дробь; когда эксцентриситет эллипса уменьшается, кривая становится все более похожей на окружность; в окружности фокусы совпадают, эксцентриситет обращается в нуль. Напротив, если в гиперболе эксцентриситет начинает возрастать, то ветки гиперболы становятся все менее и менее искривленными и приближаются друг к другу. Это соответствует тому, что секущая плоскость, оставаясь параллельной самой себе, приближается к вершине конуса; в момент, когда плоскость переходит через вершину, обе ветки соединяются, и гипербола вырождается в две прямые - две образующие конуса.

Фокусы конического сечения в приложениях математики играют важную роль в следующем отношении. Если мы соединим любую точку С кривой с ее фокусами (фиг. 8 и 9), то нормаль MN (или перпендикуляр, см. ниже отдел VI) к кривой в точке С делит угол между FC и F′С пополам. Если поэтому мы представим себе светящуюся точку в фокусе F, то луч, идущий по FC, отразится от кривой в направлении CF′; таким образом, все лучи, выходящие из одного фокуса, сойдутся в другом фокусе; но в эллипсе, это схождение будет действительное, а в гиперболе - мнимое. В параболе же все лучи, выходящие из фокуса, отразившись от кривой, становятся параллельными оси. Параболические зеркала употребляются для превращения сходящихся лучей в параллельные и обратно.

Главное же значение конических сечений в прикладном знании заключается в том, что материальная точка, которая движется вследствие притяжения к неподвижному центру, действующего по закону Ньютона, совершает свое движение по одному из конических сечений. От величины и направления начальной скорости зависит, будет ли орбита эллипсом, гиперболой или параболой. Недаром говорили, что Кеплер не открыл бы законов движения небесных светил, если бы древние не разработали учения о конических сечениях.

Мы не исчерпали здесь, конечно, даже важнейших свойств конических сечений; но многие из них мы еще укажем, когда придем к этим замечательным кривым с других точек зрения; другие же свойства читатель может найти в специальных сочинениях.

Коническими сечениями не исчерпываются высшие кривые, которые встречаются в классической геометрии. Грекам принадлежат еще квадратрикса Гипиаса Эллийского, конхоида Никомеда, циссоида Диоклесса, спираль Архимеда и другие кривые; но они не объединены здесь общей руководящей идеей, в мы предпочитаем сказать о них в другом месте.

III. Руководящие идеи аналитической геометрии.

Методы классической геометрии чужды какого бы то ни было алгебраического оттенка. Греки, как известно, не владели алгеброй, а, напротив, часто облекали в геометрическую форму то, что мы в настоящее время относим к алгебре. Вторжение алгебры в область геометрического исследования составило новую эпоху в истории геометрии и вызвало в этой науке новый мощный подъем.

Единственная форма вычисления, которую мы находим у Евклида и Аполлония, это - пропорции; но даже учение о пропорциональности, как оно создано было Евдоксом, носит в греческой литературе своеобразный характер, обходящий понятие о числе.

Связь между геометрией и алгеброй впервые устанавливают арабы. Если греки в своих построениях справлялись с уравнениями второй степени геометрически, то у арабских писателей мы находим уже эти уравнения в чистом виде; более того, арабские математики обнаруживают постоянную склонность сводить задачи на построение к решению алгебраических уравнений. Эти приемы от арабов перешли к итальянским математикам эпохи Возрождения; у Леонарда Пизанского, у Региомонтана, у Пачиолли мы постоянно встречаем геометрические задачи на построение, которые они решают алгебраически, т. е. сводят решение задачи к разысканию некоторых неизвестных, определяемых одним или несколькими уравнениями. Тем не менее, отцом приложения алгебры к геометрии обыкновенно считают знаменитого французского математика Виета (см. Алгебра, II. 91/94); его знаменитая книга "In artem analyticum isagoge" (1591) содержит как первое систематическое изложение начал символической алгебры, так и первую попытку систематически изложить приложения алгебры к геометрии, т. е. систематически указать методы построения алгебраических выражений. Таким образом приложения алгебры к геометрии развивались неразрывно с ходом развития самой алгебры; но приложения эти всегда сводились к следующему основному принципу: для решения геометрической задачи на построение та или иная геометрическая величина (обыкновенно отрезок) принималась за неизвестную; составлялось уравнение, от которого эта неизвестная зависит; это уравнение разрешалось, и полученное выражение воспроизводили графически - строили. Этими методами был, несомненно, расчищен и подготовлен путь к аналитической геометрии; но прямое зарождение последней знаменуется существенно новой идеей, почти одновременно высказанной двумя великими французскими математиками Декартом и Ферма; эта идея заключается в геометрической интерпретации неопределенного уравнения, связывающего две переменные величины - координаты точки.

Под координатами точки разумеют те величины, которыми на данном геометрическом образе определяется положение ее; так, например, если мы на прямой или на кривой линии фиксируем некоторую постоянную точку О, то положение всякой другой точки А на этой линии будет известно, если будет задано расстояние точки А от начальной точки О, отсчитываемое по длине этой линии, иначе говоря, если будет задана длина дуги OA этой линии. Эта величина и представляет собой координату точки на нашей линии. Чтобы этой координатой положение точки действительно определялось вполне, к длине отрезка OA должен быть присоединен знак, который указывал бы, в какую сторону от точки О нужно отложить заданную длину, чтобы прийти к точке А. Всем известно, что положение точки на поверхности земли определяется ее долготой и широтой; долгота и широта представляют собой координаты точки на земной поверхности.

Декарту принадлежит очень простой метод для определения положения точек на плоскости при помощи длин двух отрезков - абсциссы и ординаты точки. Сущность этого метода вполне выяснена в статье "Высшая математика" (XII, 66/69), и мы не будем здесь к ней возвращаться. Идея координации, конечно, не нова, зародыши ее можно найти еще у греческих геометров. Ганкель приводит целый ряд средневековых авторов по математике и астрономии, у которых эта идея выражена со всею возможною ясностью. Не в введении понятия о координатах заключается заслуга Декарта, а в том геометрическом истолковании, которое он дал каждой зависимости между двумя координатами точки.

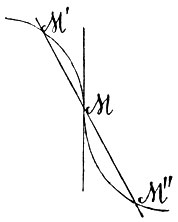
Положим, что между координатами y и x установлена некоторая зависимость, так что значение y определяется значением x, т. е. y есть функция от х:

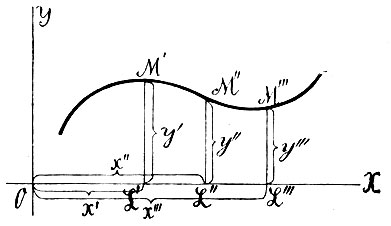
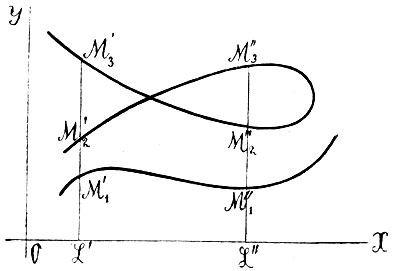
Понятие о функции (см. функция) мы предполагаем здесь совершенно усвоенным; здесь заметим только, что самая идея Декарта немало содействовала установлению и уяснению этого понятия. Положим для простоты, что f(x) в соотношении (7) есть однозначная непрерывная функция. Если мы в этом соотношении дадим x значение x′, то оно даст для у некоторое определенное значение у′; пара координат (x′, у′) определит некоторую точку M′ (фиг. 11); дадим теперь x некоторое другое значение x″; соотношение (7) даст для этого соответствующее значение у; координаты (x″, y″) определят точку М″; если теперь возьмем произвольно x′″, то ему будет соответствовать ордината у′" и точка М′″; мы можем получить таким образом неограниченный ряд точек, которые будут тем чаще следовать одна за другой, чем гуще мы будем брать значения независимой переменной x; если мы представим себе, что переменная x проходит непрерывно через все доступные ей значения, то соотношения у определят непрерывный ряд точек - кривую; об этой кривой говорят, что она выражается уравнением (7). Таким образом, каждое уравнение вида (7) выражает некоторую кривую на плоскости. Если f(x) есть неоднозначная функция, то каждому значению x отвечает не одна, а несколько точек; например, если f(x) есть трехзначная функция, то каждому значению x′, x″, x′″ отвечают три точки (M′₁, M′₂, M′₃), (M″₁, М″₂, М″₃), (M′″₁, M′″₂, М′″₃) (фиг. 12); в этом случае уравнение (7) выражает кривую, состоящую из нескольких веток; эти ветки могут иногда соединяться, как верхние две на фиг. 12, могут иногда располагаться изолированно, как нижняя и верхняя кривая на фиг. 12.

Фиг. 11

Фиг. 12

В соотношении (7) ордината y выражена, как явная, непосредственно заданная функция от абсциссы х. Соотношение между координатами может быть выражено уравнением более общего вида:

связывающим координаты x и у; но и в этом случае каждому значению x отвечает одно или несколько значений у; разрешая это уравнение, мы приведем его к виду (7). Уравнение вида (8) также выражает некоторую линию на плоскости.

Обратно, если дана некоторая кривая линия, например изображенная на фиг. 11 или 12, то каждому значению абсциссы x точки этой линии отвечает одно или несколько значений y; ордината y представляет собой, таким образом, некоторую функцию абсциссы x, и кривой соответствует уравнение вида (7) или (8).

Итак, каждое уравнение вида (8) выражает некоторую кривую на плоскости и, обратно, каждая кривая выражается некоторым уравнением этого вида. Координаты каждой точки кривой удовлетворяют этому уравнению и, обратно, каждая точка, координаты которой удовлетворяют уравнению, лежит на кривой. Это есть уравнение кривой. Так как по этому уравнению можно воспроизвести все точки кривой, то в нем необходимо содержатся и все свойства кривой; исследование кривой сводится к исследованию этого уравнения между координатами точки.

Мы старались отчетливо выразить эту идею Декарта, несомненно, представляющую собой одно из величайших завоеваний математической мысли, переносящее в алгебру и анализ центр тяжести геометрического исследования. Эти идеи получили выражение и развитие в небольшом по объему сочинению "Геометрия", опубликованном Декартом в 1637 г., и долгое время они связывались исключительно с его именем. Однако в последнее время обнаружилось, что Ферма владел этими идеями уже в 1629 г.; об этом свидетельствует сохранившееся письмо Ферма к Робервалю, а главным образом посмертные мемуары Ферма ("Isagoge ad locos planos et solidos"); оставлять поэтому имя Ферма в тени было бы тем более несправедливо, что в этих мемуарах идея аналитической геометрии разработана с значительно большей полнотой, чем у Декарта. Но и здесь следует подчеркнуть, что зародыши этой идеи можно найти уже в глубокой древности. В самом деле, возвратимся, например, к соотношению (3), которым парабола определялась еще до Аполлония, правда, в геометрической форме. Будем рассматривать прямые АС и AR (фиг. 6), как оси координат, и отрезки АС и CD примем за абсциссу x и ординату у точки на кривой; постоянный отрезок AR обозначим через р. Соотношение (3) древние выражали таким образом, что квадрат, построенный на CD, равен прямоугольнику, построенному на АС и AR. Если мы, однако, выразим это соотношение в числах при помощи принятых сейчас обозначений, то получим:

как уравнение параболы. Таким же образом соотношение (4), служащее общим определением конических сечений у Аполлония, в новых обозначениях имеет вид

это и есть общее уравнение конических сечений.

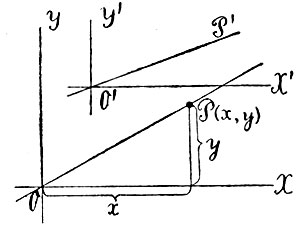
В основе Декартовой координации лежат две неподвижные пересекающиеся прямые - оси координат; эти оси могут быть выбраны, конечно, произвольно; каждой системе осей отвечает своя координация. Иными словами, каждая точка относительно одних осей будет иметь одни координаты, относительно других - другие. Весьма простая, но в то же время и основная задача аналитической геометрии заключается в следующем: точки плоскости отнесены к некоторой одной системе координат, затем выбраны новые оси; как выразятся старые координаты каждой точки через новые и обратно? Простейший случай мы имеем возможность здесь же исчерпать. Положим, что плоскость была отнесена к осям ОХ и OY (фиг. 13); пусть x, y будут координаты произвольной точки М, а a, b - координаты некоторой определенной точки O′. Через эту последнюю проведены прямые O′Х′ и O′Y′, параллельные старым осям; координаты точки М относительно новой системы осей обозначим через x′, y′ (см. чертеж). Одного взгляда на чертеж достаточно, чтобы убедиться, что

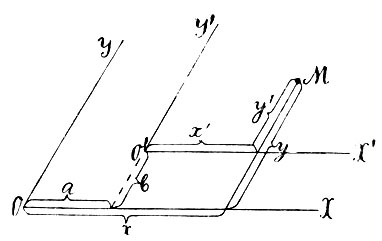
Фиг. 13

Таковы в этом случае простые формулы преобразования координат; простота их обусловливается тем обстоятельством, что новые оси параллельны первоначальным. При ином относительном положении осей они становятся сложнее, но всегда имеют вид:

где коэффициенты k, l, m, n зависят от относительного положения новых и старых осей.

Учение о преобразовании координат всегда начинает собой аналитическую геометрию и имеет капитальное значение потому, что от выбора координат в большой мере зависит и форма уравнения кривой: целесообразное избрание осей часто приводит к значительному упрощению уравнения.

Способ координации точек на плоскости, указанный Декартом, отнюдь не является единственным. Из других методов координации важнейшее значение имеют полярные координаты. Здесь положение точки М на плоскости определяется относительно неподвижной оси ОХ (полярной оси, фиг. 14) и постоянной точки на ней O (начала). На том же чертеже показаны и Декартовы координаты той же точки М. Полярными координатами служат расстояние r=ОМ и угол φ=MON; соотношение между r и φ вида:

выражает линию на плоскости. Положение точки на плоскости может определяться ее расстояниями от двух неподвижных точек (биполярные координаты), пересечением проходящих через нее конических сечений (эллиптические координаты) и многочисленными другими способами. Ламе (G. Lamé) дал общую теорию координации ("Leçons sur les coordonées courvilignes"), которая служит по настоящее время основанием наиболее общих методов аналитического исследования кривых. Мы укажем здесь только основную идею этих общих исследований, представляющую собой непосредственное развитие идей Декарта-Ферма.

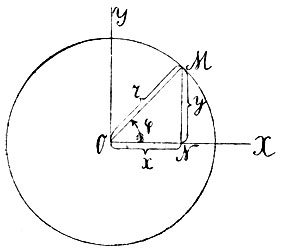
Фиг. 14

Пусть t будет совершенно произвольная переменная, и пусть

будут два уравнения, определяющие координаты x, у точки на плоскости в зависимости от t. Тогда каждому значению t отвечает пара значений x, у, т. е. отвечает точка на плоскости; совокупность всех точек, отвечающих всем доступным для переменной t значениям, образуете линию; говорят, что эта линия выражается уравнениями (14) в зависимости от параметра t. Эти два "параметрические" уравнения заменяют одно Декартово уравнение (8); и это последнее уравнение можно получить, исключая параметр t из этих уравнений. Эти идеи вполне выясняются на следующем простом примере. Рассмотрим окружность, описанную радиусом r из начала прямоугольных Декартовых координат (ф. 14). Из прямоугольника MON мы видим, что

Это и будут параметрические уравнения окружности, выражающие координаты точки на окружности через параметр φ. Чтобы получить Декартово уравнение окружности, нужно из них исключить φ; возвышая для этого уравнения (15) в квадрате и складывая их почленно, получим:

Выяснив с надлежащей обстоятельностью исходные идеи аналитической геометрии на плоскости, мы можем ограничиться относительно распространения этих идей на трехмерное пространство тем, что изложено в статье "Высшая математика" (XII, 73/74), и здесь дадим только сводку результатов.

Положение точки в пространстве определяется тремя координатами; в системе декартовых прямоугольных координат этими координатами (x, y, z) служат расстояния точки от трех взаимноперпендикулярных плоскостей, взятые с надлежащими знаками. Каждое уравнение вида:

связывающее эти координаты, выражает поверхность; два уравнения вида:

выражают кривую в пространстве. Исследование линий и поверхностей сводится, таким образом, к исследованию уравнений, которыми они выражаются.

IV. Учение об алгебраических кривых.

При аналитическом исследовании плоских кривых естественным основанием для классификации последних должна служить форма уравнения кривой. Но, как мы сказали, эта форма в большой мере зависит от выбора координат. В основу классификации должны быть, естественно, положены такие свойства уравнения, которые не меняются при преобразовании координат определенной системы, например декартовых координат. Плоские кривые делятся, прежде всего, на алгебраические и трансцендентные; алгебраическими кривыми называются такие, в которых левая часть уравнения (8) представляет целую алгебраическую функцию от x и y, т. е. полином, расположенный по степеням x и y. Кривые же, уравнения которых не могут быть приведены к этому виду, называются трансцендентными; мы ниже приведем несколько примеров трансцендентных кривых, а теперь обратимся к алгебраическим кривым.

Каким бы преобразованиям мы ни подвергали декартовы координаты, степень уравнения, выражающего алгебраическую кривую, не изменяется; эта степень представляет нечто для алгебраической кривой неизменное (инвариант), характерное; эту степень называют поэтому порядком кривой. Покажем, что прямая есть линия первого порядка, т. е. выражается уравнением первой степени. Так как степень уравнения, как уже было сказано, не зависит от выбора осей, то мы будем в дальнейшем пользоваться прямоугольными координатами, т. е. такими, в которых оси координат образуют прямой угол.

Пусть ОР будет прямая, проходящая через точку пересечения осей O, или начало координат, как ее принято называть (фиг. 15); пусть P(x, у) будет прозначим тангенс угла α, который прямая образует с осью абсцисс. Теперь из прямоугольного треугольника с катетами x и у ясно, что для любой точки прямой P имеет место соотношение:

это и есть уравнение прямой, проходящей через начало координат; коэффициент при xk называют угловым коэффициентом прямой. Положим теперь, что нам нужно составить уравнение прямой O′P′, не проходящей через начало координат. Пусть а, b будут координаты произвольной точки O′ этой прямой; проведем через нее две прямые O′Х′ и O′Y′, параллельные осям, и примем эти прямые за оси новой системы координат. Так как теперь прямая О'P' проходит через начало, то в новых координатах (x′, y′) ее уравнение будет иметь форму (19), т. е. будет.

Но при помощи формул (11) мы можем легко перейти от новых координат (x′, y′) к первоначальным (x, y); ясно, что уравнение примет вид

Это есть уравнение прямой, проходящей через данную точку (а, b) и образующей с осью абсцисс угол α(tgα=k). Прямая таким образом, всегда выражается уравнением первой степени, т. е. представляет собой линию первого порядка. Предыдущее рассуждение падает только в том случае, если прямая перпендикулярна к оси абсцисс: в этом случае коэффициент k в уравнениях (19) и (20) обращается в бесконечность; треугольника, из которого мы получили соотношение (19), вовсе нельзя составить. Но если PQ есть такая прямая (перпендикулярная к оси абсцисс) и а есть абсцисса точки Q, в которой она встречает ось абсцисс, то и все точки прямой PQ имеют ту же абсциссу, т. е. для всех точек этой прямой

Это и есть уравнение прямой, параллельной ось ординат; оно также представляет собою уравнение первой степени.

Обратно, всякое уравнение 1-ой степени может быть приведено либо к виду (20), либо к виду (21). В самом деле, наиболее общий вид уравнения первой степени между двумя переменными (х, у) есть:

Если в этом уравнении коэффициент B отличен от нуля (т. е. если в нем не отсутствует вовсе у), то оно может быть решено относительно у, и тогда примет вид:

Пусть a, b будет пара значений переменных x и y, удовлетворяющих этому уравнению; мы будем тогда иметь тождество:

Вычитая это тождество из уравнения (23), мы приведем его к виду (20); оно выражает собой, следовательно, прямую, проходящую через точки (а, b) и имеющую коэффициент наклона k. Если в уравнении (22) члена, содержащего у, нет, то оно приводится к виду (21), т. е. выражает прямую, параллельную оси ординат.

Фиг. 15

Мы преднамеренно остановились несколько подробнее на этом анализе, так как, при всей своей простоте, он является типичным для аналитического исследования геометрических образов. Уравнений прямой у Декарта нет, у Ферма они приведены в несколько иной форме. В современных сочинениях по аналитической геометрии учение о прямой изучает аналитически все те вопросы, которые в классической геометрии решаются графически: там решают задачи о построении прямых, перпендикулярных или параллельных данным прямым, о проведении биссекторов углов между прямыми, вообще, о проведении прямых по разным заданиям; здесь задача сводится к тому, чтобы по аналогичным заданиям составить уравнения соответствующих прямых и, обратно, по уравнению прямой судить об ее положении. Мы обратим здесь внимание еще на одно только обстоятельство. В наиболее общем уравнении прямой (22) имеются как будто 3 произвольных коэффициента; в действительности их, однако, только 2, так как на один из коэффициентов мы всегда можем уравнение разделить. Этому факту отвечает то обстоятельство, что прямая определяется двумя заданиями, в частности, двумя своими точками.

Обращаясь теперь к кривым второго порядка, заметим прежде всего, что наиболее общее уравнение этого рода кривой имеет вид:

Здесь коэффициентов 6, но так как один из них мы можем делением свести к 1, то независимым коэффициентов остается 5. Соответственно этому кривая 2-го порядка наиболее общего вида определяется 5 заданиями, в частности 5 своими точками.

Обращаясь к вопросу о возможной форме кривой 2-го порядка, заметим, прежде всего, что левая часть может иногда распадаться на два рациональных множителя 1-ой степени, т. е. уравнение (25) иногда может быть представлено в виде:

Но так как произведение двух множителей обращается в нуль в том и только в том случае, если один из множителей обращается в нуль, то уравнение (26) распадается на 2 уравнения

т. е. выражает две прямые. Говорят, что кривая 2-го порядка распадается в этом случае на 2 прямые или "вырождается" в две прямые. Интерес сводится, таким образом, к определению формы нераспадающейся кривой второго порядка. Весь вопрос исчерпывается в этом случае следующей теоремой: уравнение всякой нераспадающейся кривой второго порядка надлежащим преобразованием координат всегда может быть приведено к виду (10); а так как это последнее уравнение, в зависимости от значения коэффициента h, выражает то или иное коническое сечение, то всякая кривая второго порядка представляет собой коническое сечение (даже распадающаяся, так как две прямые также могут представлять сечение конической поверхности плоскостью). Аналитическая геометрия, таким образом, приводит к коническим сечениям, как к первой по простоте после прямых категории кривых линий.

Мы остановимся еще на некоторых деталях. Первый шаг в деле исследования уравнения (25) заключается в том, чтобы решить, от каких членов это уравнение может быть освобождено надлежащим преобразованием координат. Оказывается, что надлежащим поворотом осей уравнение всегда может быть освобождено от члена, содержащего xy. Интерес исследования сосредоточивается на том, может ли уравнение быть также освобождено от членов, содержащих координаты x, у в первой степени; это иногда бывает возможно, иногда невозможно. Если это возможно, то уравнение принимает вид

Существенная особенность этого уравнения заключается в следующем: если ему удовлетворяют значения переменных (а, b), то ему удовлетворяют в этом случае также значения (-а, -b) иначе говоря, если на кривой лежит точка М (а, b), то на ней лежит также точка М′ (-а, -b), симметричная точке М относительно начала; начало служит серединой отрезка MM′, т. е. серединой любой хорды кривой, через него проходящей; начало служит центром симметрии кривой. Итак, если уравнение кривой может быть приведено к виду (28), то она имеет центр. Если здесь F не равно 0 (случай F=0 мы рассмотрим ниже), то уравнение можно разделить на F, и оно примет вид

Отсюда следует, что коэффициенты A′ и В′ не могут быть оба отрицательными, так как тогда левая часть уравнения имела бы отрицательное значение. Вновь возможны, таким образом, 2 случая, - когда оба коэффициента имеют положительные значения и когда один имеет положительное, другой отрицательное значение. Если поэтому мы абсолютные величины коэффициентов A′ и В′ выразим для симметрии через 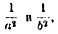то уравнение (29) примет одну из двух форм:

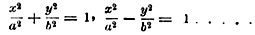
(30)

Как уже было выяснено в статье "Высшая математика", первое из этих уравнений выражает эллипс, второе - гиперболу; в том и в другом случае оси кривой лежат на осях координат и имеют длины 2a и 2b. Впрочем, по виду этих уравнений можно сразу усмотреть, что в первом из них координата x по абс. величине не может превышать а, а координата y не может по абс. величине превышать b; уравнение выражает ограниченную кривую - эллипс. Во втором уравнении обе координаты могут принимать сколь угодно большие значения, как это имеет место в гиперболе.

Любопытно сравнить уравнения (30) с аналогичными, которые получаются, когда мы в правой части вместо 1 напишем нули; это соответствует упомянутому выше случаю, когда в уравнении (28) F=0. Мы получим.

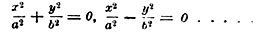
(31)

Левая часть первого из этих уравнений состоит из двух положительных слагаемых, она может поэтому обратиться в 0 только в том случае, если каждое слагаемое отдельно обращается в нуль. Иными словами, уравнению удовлетворяет только одна пара действительных значений переменных x=0, y=0, т. е. оно выражает только одну точку - начало координат. Что касается второго уравнения, то оно распадается на два.

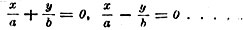
(32)

Не трудно убедиться, что это две прямые, проходящие через противоположные вершины F,J и G,H прямоугольника (фиг. 5), построенного на осях соответствующей гиперболы. Эти замечательные прямые называются асимптотами гиперболы, обе ветви кривой медленно и неограниченно приближаются к асимптотам с обеих сторон, никогда их, однако, не достигая.

Возвратимся еще к первому из уравнений (30); ему удовлетворяет, кроме одной пары действительных значений x, y, еще бесчисленное множество комбинаций мнимых значений. Это обстоятельство привело к идее ввести в рассмотрение так называемые "мнимые точки". Под мнимой точкой разумеют только пару мнимых значений координат, никакого пространственного образа с этим понятием не соединяется. Когда говорят, что на том или ином образе лежит мнимая точка, то это лишь по форме геометрическое выражение того факта, что пара мнимых значений координат удовлетворяет уравнению геометрического места. Так как левая часть 1-го уравнения (30) может быть разбита на два мнимых множителя, то она распадается на уравнения

и говорят, что оно выражает две "мнимые прямые", проходящие через одну действительную точку - начало координат. Эти фиктивные образы, за которыми не скрывается ничего, кроме чисел и числовых соотношений, нередко оказывают значительные услуги геометрическому исследованию: при помощи их многие теоремы получают более общее и простое выражение; благодаря им часто бывает возможно избежать расчленения вопроса на множество частных случаев; вообще, как вспомогательное средство, эти мнимые геометрические образы часто оказывают те же услуги, что мнимые числа в алгебре и анализе. Максимилиан Мари, Белавитис и др. показали, что эти идеи можно использовать и в интересах прямого геометрического исследования.

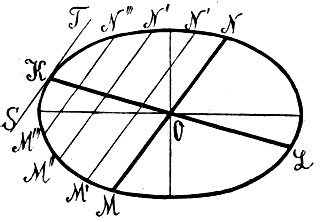
Уравнения центральных кривых второго порядка - эллипса и гиперболы - принимают простую форму (30), когда начало координат совпадает с центром кривой, а оси координат - с осями кривой. Замечательное свойство осей, которое непосредственно бросается в глаза, заключается в следующем: если мы проведем произвольную хорду, параллельную одной из осей, то середина этой хорды лежит на другой оси. Можно сказать, что одна из осей представляет собой геометрическое место середин всех хорд, параллельных другой оси. Это свойство хорд допускает обобщение: если мы проведем хорды, параллельные любому диаметру кривой, то середины их располагаются на другом диаметре; такие два диаметра называются сопряженными; на фиг. 16 KL и MN суть сопряженные диаметры эллипса. Замечательно, что это соотношение взаимное: хорды, параллельные любому из двух сопряженных диаметров, делятся пополам вторым диаметром. Оси кривой, как мы уже сказали, представляют собой пиру сопряженных диаметров; но это единственная пара сопряженных диаметров, которые взаимно перпендикулярны. Замечательно, что уравнение центральной кривой 2-го порядка принимает форму (30), если мы направим оси по любым двум сопряженным диаметрам кривой.

Фиг. 16

Все приведенные здесь рассуждения относительно эллипса и гиперболы связаны с тем обстоятельством, что уравнения их могут быть освобождены от членов, содержащих координаты в первой степени, т. е. могут быть приведены к виду (30). Но, как мы уже указали выше, это не всегда возможно; некоторые уравнения второй степени не могут быть освобождены одновременно от обоих членов, содержащих x и y в первой степени; соответствующая кривая не имеет центра. Но оказывается, что в этом случае уравнение всегда может быть приведено к виду (9), так что кривая представляет собой параболу: парабола есть единственная кривая второго порядка, не имеющая центра. Вместе с тем в параболе не может быть речи о диаметрах в том смысле, как мы о них говорили в случае эллипса или гиперболы, т. е. как о хордах, проходящих через центр. Но замечательно, что и здесь, если мы возьмем совокупность параллельных хорд, то середины их лежат на одной прямой. Это обстоятельство и принимают поэтому за точку отправления для общего определения диаметра кривой второго порядка: под диаметром кривой второго порядка разумеют геометрическое место середин системы параллельных между собою хорд. - В центральных кривых (эллипсах и гиперболах) диаметры всегда проходят через центр; в параболе они всегда параллельны оси. В центральной кривой каждому диаметру отвечает сопряженный диаметр: в параболе диаметр сопряжен лишь с системой хорд, через середины которых он проходит.

В центральной кривой построение диаметра, сопряженного с данным, не представляет никаких затруднений: для этого достаточно провести хорду M′N′ (фиг. 16), параллельную данному диаметру MN, и ее середину P′ соединить с центром кривой. В параболе построить диаметр, сопряженный с данным направлением хорд, конечно, также не представляет затруднений: для этого достаточно соединить середины двух хорд этого направления. Труднее определить направление хорд, сопряженных с данным диаметром. Мы еще скажем об этом несколько слов ниже.

В тесной связи с учением о сопряженных диаметрах конических сечений стоит вопрос о касательных. Во скольких точках прямая может пересекать кривую 2-го порядка? Чтобы ответить на этот вопрос, заметим, что координаты общих точек двух линий должны удовлетворять уравнениям обеих линий; мы найдем поэтому эти точки, если соединим уравнения обеих кривых в одну систему и совместно их разрешим. Если мы разыскиваем пересечение прямой в кривой второго порядка, то система состоит из одного уравнения первой степени и одного - второй степени. Решая такую систему совместно, мы получаем 2 пары решений - действительных или мнимых. Сообразно этому прямая пересекает кривую второго порядка в двух точках - действительных или мнимых. Иногда обе точки пересечения сливаются в одну - прямая обращается в касательную к кривой.

Положим что секущая M′N′ (фиг. 16) перемещается параллельно самой себе: она дает все меньшие и меньшие хорды M′N′, M″N″, M′′′N′′′ ... и в пределе, когда точки М и N сливаются в одну точку K, обращается в касательную к кривой в этой точке. Следовательно, касательная к коническому сечению параллельна хордам, сопряженным с тем диаметром, который проходит через точку касания.

Отсюда ясно, как построить касательную в какой-либо точке K центрального конического сечения (фиг. 16). Для этого проводим через точку K диаметр, строим, как было указано выше, диаметр MN, сопряженный с ним, а затем через точку K проводим прямую параллельную MN. Это построение не пригодно для параболы (фиг. 17), так как здесь диаметр KL параллелен оси, и построить сопряженные ему хорды этим способом нельзя. Здесь для построения касательной в точке K соединяем эту точку с фокусом F; биссектриса KG угла FKL, как мы уже знаем (стб. 12), будет нормалью к кривой; перпендикуляр KS к KG будет служить касательной. Чтобы найти фокус, если он не был известен, делаем обратное построение: берем произвольную хорду MN, через середину ее P проводим прямую PQ, параллельно оси параболы; это будет диаметр, сопряженный с хордой MN. Если этот диаметр встречает кривую в точке Q, то прямая QT, параллельная MN, служит касательной к кривой; перпендикуляр к ней QR должен делить пополам угол PQF. Поэтому, чтобы построить фокус, остается провести луч QF, образующий с QR угол, равный RQP. Заметим, что это построение касательной при помощи фокуса и фокуса при помощи касательной пригодно также для центральных кривых 2 порядка; кроме того, нужно сказать, что для построения касательной существуют еще многие другие достаточно простые приемы.

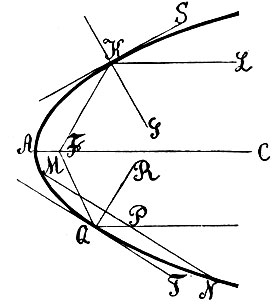
Фиг. 17

В аналитическом развитии теории кривых второго порядка весь этот материал разрабатывается, конечно, алгебраическими средствами; устанавливаются критерии, дающие возможность определить тип кривой по ее уравнению; указываются методы, как по уравнению кривой найти ее центр и оси, как привести уравнение к простейшему виду (30) или (9), как составить уравнения сопряженных диаметров, касательной и нормали в каждой точке кривой, как определить координаты фокусов, уравнения директрис и т. д.

Мы займемся, однако, еще одним примыкающим сюда геометрическим вопросом, имеющим большую важность. Мы показали, как провести касательную к коническому сечению из точки, лежащей на самой кривой. Положим, что из точки А (фиг. 18) нужно провести касательную к коническому сечению. Анализ обнаруживает, прежде всего, что каждое коническое сечение делит плоскость на две части: внутреннюю, из точек которой нельзя провести касательную к кривой, - и внешнюю, из каждой точки которой выходят две касательные к кривой. Итак, положим, что нам дана точка A вне кривой; из нее выходят две касательные к кривой AM и AN; как их построить? Прямую MN, соединяющую точки касания выходящих из точки A касательных к кривой, называют полярой точки А, точку же А называют полюсом прямой MN. Если бы мы умели построить поляру каждой точки, то вопрос о проведении касательных из внешней точки был бы решен: достаточно было бы построить поляру MN данной точки A и точки M,N ее пересечения с кривой соединить с A; это и будут касательные. Но как построить поляру данной точки?

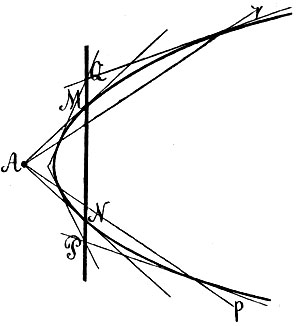
Фиг. 18

Два обстоятельства играют здесь решающую роль. Во-первых, если дана прямая MN, пересекающая коническое сечение, то построить ее полюс не представляет затруднений: для этого достаточно провести касательные в точках М и N ее пересечения с кривой; точка пересечения последних A и есть полюс прямой. Второе обстоятельство заключается в следующей основной теореме: если какая-либо прямая Aq проходит через полюс A прямой MN, то ее полюс Q лежит на поляре MN этой точки А (фиг. 18). Несколько иначе: когда прямая Aq вращается вокруг неподвижной точки А, то ее полюс перемещается по поляре MN этой точки. Ясно, следовательно, что и, наоборот, когда точка Q движется по прямой MN, то поляра Aq этой точки вращается вокруг полюса A прямой MN. Из этих соображений непосредственно вытекает простой метод построения поляры данной точки А: мы проводим через нее две прямые, пересекающие коническое сечение, скажем Ар и Aq; затем строим полюсы P и Q этих прямых; прямая PQ и будет полярой точки А.

Вопрос о построении касательных к коническому сечению из внешней точки этим вполне исчерпан. Но в связи с этим стоят некоторые соображения принципиальной важности. Предыдущее определение устанавливает понятие о поляре только для таких точек, которые лежат вне конического сечения. Но указанное выше построение находит себе применение и в том случае, когда точка A лежит внутри кривой (фиг. 19). Мы и в этом случае можем провести через точку А две прямые pp′ и qq′, пересекающие кривую, найти их полюсы P и Q и последние соединить. Замечательно то, что мы при этом получаем одну и ту же прямую PQ, как бы ни были взяты исходные прямые pp′ и qq′. Эта прямая PQ принимается за поляру точки А. Таким образом устанавливается понятие о поляре как для внутренней, так и для внешней точки кривой и притом устанавливается при помощи одного и того же построения. Что дает это построение, когда точка лежит на самой кривой? Если мы станем строить поляру точки p (на фиг. 19) тем же способом, мы должны будем провести через точку p две секущие pp′ и pp″, найти их полюсы и соединить последние. Но полюс прямой pp′ будет лежать в пересечении касательных в точках p и p′, он будет лежать, следовательно, на касательной pP в точке p. Но так как через ту же точку p кривой проходит вторая вспомогательная прямая pp″, то и ее полюс также лежит на касательной Pp, а потому и самой полярой точки p будет служить касательная к кривой в этой точке; полярой точки на кривой служит касательная к кривой в этой точке.

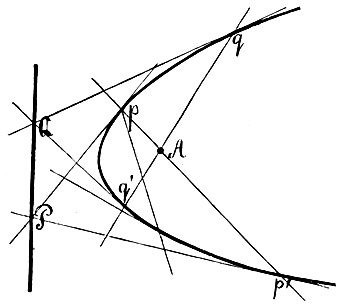
Фиг. 19

Подобно тому, как каждой точке на прямой теперь соответствует поляра, каждой прямой, даже не пересекающей кривой, отвечает полюс: для его разыскания достаточно построить поляры любых двух ее точек: пересечение этих поляр и будет служить полюсом данной прямой.

Учение о полюсах и полярах имеет большое теоретическое значение с различных точек зрения. Прежде всего, мы можем на полярах выяснить роль мнимых элементов в аналитической геометрии. Если пользоваться мнимыми образами, то исходное определение поляры может быть принято за общее определение ее. Дело в том, что аналитически из любой точки плоскости, не лежащей на данном коническом сечении, можно к последнему провести две касательные; но эти касательные будут действительные, если точка лежит вне конического сечения, и мнимые, если она лежит внутри его. И тонки касания будут в первом случае действительные, во втором мнимые. Поляра данной точки есть прямая, соединяющая точки касания (действительные или мнимые) двух касательных, проведенных из данной точки к коническому сечению; когда точка лежит на коническом сечении, обе касательные сливаются в одну; она же служит и полярой к кочке касания. Обратно, каждая прямая пересекает коническое сечение в двух точках, действительных или мнимых; через каждую из этих точек проходит касательная к кривой, соответственно действительная или мнимая; точка пересечения двух касательных оказывается всегда действительной - это есть полюс данной прямой. В согласии с этим уравнение поляры данной точки всегда имеет один и тот же вид, где бы ни лежал полюс. Если, например, кривая имеет уравнение вида (30), то уравнение поляры точки x₁, y₁ имеет соответственно вид:

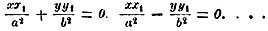
(34)

Если точка лежит на кривой, то уравнения (34) выражают касательную - соответственно - к эллипсу или гиперболе.

Другая сторона дела - это соответствие между полюсом и полярой. В отделе I мы указали на геометрическое соответствие, как на одну из основных категорий геометрических изысканий. Но соответствие, о котором была речь там, это соответствие точек; оно заключается в том, что каждой точке, скажем, плоскости мы относим в качестве соответствующей некоторую другую точку этой плоскости. Здесь каждое коническое сечение устанавливает некоторое соответствие другого рода: каждой точке отвечает прямая - ее поляра, каждой прямой - точка, ее полюс. В возможности такого сопряжения коренится источник глубокой аналогии между точками и прямыми - так называемое начало двойственности или взаимности. С этими идеями мы еще встретимся ниже в отделе, посвященном проективной геометрии.

В этом кратком обзоре аналитической теории кривых второго порядка мы имели возможность коснуться только самых существенных вопросов; мы вынуждены обойти даже учение о софокусных, подобных и гомотетичных конических сечениях, о пучках в связках их; мы должны были ограничиться теми сторонами дела, которые выясняют общую идею аналитического исследования кривых. Обращаясь теперь к кривым более высоких порядков, мы вынуждены ограничиться еще более краткими указаниями, главным образом, такими, которые выясняют, как быстро здесь все вопросы усложняются.

Начнем с вопроса о независимости точек относительно кривой. Кривая второго порядка, как мы уже упоминали выше, определяется 5 своими точками; при этом любые 5 точек, лежащих на данном коническом сечении, являются независимыми в следующем смысле этого слова: если мы из 5 точек удержим только 4, то через них можно будет провести бесчисленное множество конических сечений, пятой точки не содержащих. Дело обстоит иначе в случае кривых более высоких порядков. Общее уравнение кривой третьего порядка имеет 9 независимых коэффициентов; сообразно этому, кривая 3-го порядка должна определяться 9 точками. Так оно и имеет, вообще место; но здесь есть исключение, существенно отличающее этот случай от того, что имеет место в случае кривой 2-го порядка. Если мы возьмем 8 точек на кривой 3-го порядка, то через них можно, конечно, провести еще бесчисленное множество других кривых 3-го порядка; но все они проходят через некоторую определенную девятую точку. Более того, эти 9 точек образуют связанную группу таким образом, что всякая кривая 3-го порядка, проходящая через 8 из них, необходимо проходит через девятую. Эти зависимости еще усложняются для кривых более высоких порядков. Определение условия независимости точек на алгебраической кривой и связанных между собой групп составляет первый момент в деле общего исследования алгебраических кривых.

На нераспадающейся кривой второго порядка все точки суть обыкновенные. Это значит, если мы опишем из точки М на кривой окружность весьма малым радиусом, то она пересекает кривую в двух точках М′ и М″ (фиг. 20 а). Два радиуса MM′ и MM″ образуют при весьма малой величине этого радиуса тупой угол М′ММ″, который выпрямляется по мере уменьшения радиуса; в пределе прямые ММ′ и ММ″ сливаются в одну - в касательную к кривой, по одну сторону от которой располагается кривая. Если кривая 2-го порядка распадается на 2 прямые, то точка пересечения М этих кривых (фиг. 20 b) представляет собой единственный случай особенной точки: окружность, описанная около точки М малым радиусом, пересекает нашу линию в 4 точках. Точка M называется в этом случае двойной: если мы возьмем две точки M′ и М″ на равном расстоянии от M на одной и другой прямой, то прямая M′M″ встречает линию в этих двух точках. Если мы будем уменьшать расстояние MM′=MM″, то обе точки пересечения будут приближаться к М, хотя прямая М′М″ в касательную не обратится.

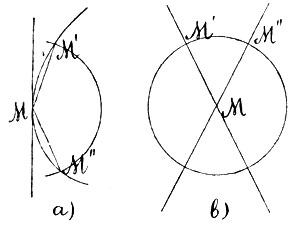
Фиг. 20

Гораздо сложнее обстоит дело в алгебраических кривых более высокого порядка. Здесь нераспадающаяся кривая может иметь и обыкновенно имеет особенные точки. Особенности эти столь разнообразны, что даже дать общее их определение геометрически представляется затруднительным. Прежде всего возможны кратные точки, в которых пересекаются или соприкасаются различные ветви кривой. Кривая n-го порядка выражается уравнением n-ой степени. Если мы расположим левую часть уравнения кривой f(x,y)=0 по восходящим степеням переменных, то она будет начинаться со свободного члена, затем будут следовать члены 1-го, 2-го, 3-го измерения и т. д. Если за начало координат принята точка на кривой, то значения x=0, y=0 должны обращать левую часть уравнения в нуль; а потому свободный член должен быть равен нулю. Обыкновенно левая часть уравнения будет при таких условиях начинаться с членов первого измерения; в этом случае начало координат будет обыкновенной точкой кривой; приравнивая нулю члены первого измерения, мы получим уравнение касательной к кривой в этой точке. Но иногда членов первого измерения может не быть, левая часть уравнения начинается с членов второй кратности; тогда начало будет двойной точкой кривой, а приравнивая члены второго измерения пулю, мы получим геометрическое место, распадающееся на две прямые; это будут две касательный к кривой в этой точке. Вообще, если функция f(x,y), составляющая левую часть уравнения кривой (8), начинается с членов k-го измерения, то начало координат служит точкой k-ой кратности этой кривой; приравнивая же нулю члены k-ой кратности, мы получим уравнение k касательных в этой точке. Но эти k касательных могут группами совпадать, некоторые из них могут оказаться мнимыми; это коренным образом влияет на характер кратной точки. На чертеже XI в статье "Высшая математика" (XII, 81) можно видеть различные виды особенных точек.

Но даже в том случае, когда O есть обыкновенная точка кривой, касательная к ней в этой точке может находиться с кривой в более или менее тесном соприкосновении. Если мы в точке М кривой (фиг. 20) повернем касательную на небольшой угол, то она пересечет кривую еще в одной точке М′, весьма близкой к М. Но если мы повернем касательную вокруг точки М на небольшой угол на кривой, изображенной на фиг. 21, то касательная пересечет кривую помимо точки М еще в двух точках, потому что кривая в точках, прилежащих к М, располагается не с одной стороны касательной, а с обеих сторон. Такого рода точка называется точкой перегиба: в зависимости от числа точек, в которых касательная при небольшом повороте пересекает кривую вблизи точки М, определяется порядок перегиба. Аналитически точка перегиба характеризуется тем, что сумма членов первого измерения входит множителем в состав более высоких групп; в так называемой простой точке перегиба группа членов первого измерения служит делителем группы членов 2-го измерения, но не делит группы 3-го измерения.

Фиг. 21

Неразлагающаяся кривая n-го порядка имеет не больше, чем 1/2(n-1)(n-2) двойных точек; в частности кривая 3-го порядка может иметь только одну двойную точку, но может иметь 9 точек перегиба. Еще Маклорен показал, что эти точки перегиба расположены таким образом, что прямая, проходящая через две из них, проходит еще через третью; таким образом получается 12 прямых, из которых каждая содержит три точки перегиба, а через каждую точку перегиба проходят четыре из этих прямых.

Роль поляр для кривых высших порядков заменяют так называемые полярные кривые. Относительно кривой n-ого порядка каждой точке отвечает кривая (n-1)-го порядка, служащая ее полярной кривой. Относительно кривой 3-го порядка, например, каждой точке отвечает полярное коническое сечение. Точки касания касательных, проведенных к кривой из данной точки, лежат на пересечении данной кривой с полярной кривой, соответствующей этой точке; этих точек пересечения в случае кривой n-го порядка будет n(n-1); сообразно этому из точки, лежащей вне кривой, можно провести к кривой n-ого порядка n(n-1) касательных; но между ними могут оказаться совпадающие и мнимые. Из точки, лежащей вне кривой 3-го порядка, можно провести к ней 6 касательных.

Классификация алгебраических кривых каждого по рядка представляет большие затруднения. Так, классификацией кривых 3-го порядка занимался еще Ньютон; но так как здесь возможны различные точки отправления, то и результаты классификации могут быть чрезвычайно различны. Так, например, Ньютон различал 72 вида кривых 3-го порядка, между тем как Плюкер (Plücker) насчитываем их 219.

Было указано много приемов, определяющих геометрически происхождение кривых высшего порядка; в большинстве случаев они основаны на проективных соображениях, и мы еще упомянем о них в своем месте. Здесь же укажем следующее образование кривых 3-го порядка, принадлежащее Грассману. Положим, что мы имеем три неподвижные прямые а, b, с и три постоянные точки A, В, С: если мы произвольную точку М соединим с точками A, В, С, то прямые MA, MB, МС пересекут неподвижные прямые a, b, с соответственно в точках А′, В′, С′. Если точка М движется таким образом, что при каждом ее положении соответствующие точки A′, B′, C′ лежат на одной прямой, то она описывает кривую 3-го порядка; и обратно, как показал Клебш (Clebsch), каждая кривая 3-го порядка может быть получена этим путем. Замечательно, что этот метод образования кривых 3-го порядка может быть распространен на алгебраические кривые любого порядка; но мы не будем на этом останавливаться.

Глубокое изучение высших алгебраических кривых тесно связано с решением сложных алгебраических вопросов; геометрическое и алгебраическое исследования идут здесь рядом, и геометрия часто оказывает такие же услуги алгебре, какие последняя оказывает геометрии.

V. Учение об алгебраических поверхностях.

Остановившись сравнительно подробно на аналитическом исследовании алгебраических кривых, мы дадим лишь краткий обзор результатов, к которым приводим применение тех же приемов к исследованию алгебраических поверхностей.

Как было выяснено в отделе III, поверхность выражается уравнением вида F(x, у, z)=0. Поверхность называется алгебраической, если она выражается алгебраическим уравнением; степень этого уравнения определяем порядок поверхности. Поверхность первого порядка, выражающаяся уравнением

представляет собою плоскость: и, обратно, каждая плоскость выражается уравнением этого вида. Аналитическая геометрия дает средства определять положение такой плоскости и положение плоскостей друг относительно друга по их уравнениям; она дает также правила, для составления уравнения плоскости по заданиям, которыми таковая определяется.

Пересечением двух плоскостей определяется прямая в пространстве. Сообразно этому прямая в пространстве выражается двумя уравнениями вида (35).

Поверхность второго порядка выражается уравнением второй степени, наиболее общая форма которого представляется в следующем виде:

Левая часть этого уравнения распадается на четыре части; первую часть представляют 3 члена, содержание квадраты координат, вторую - члены, содержащие их произведения, третью - члены первой степени, а четвертую составляет свободный член. Как и при исследовании кривых второго порядка, оказывается, что прямоугольные координаты можно всегда ориентировать таким образом, чтобы члены, содержание произведения неизвестных, исчезли. Вопрос заключается в том, возможно ли при надлежащем выборе начала освободиться также от членов первой степени. Это иногда оказывается возможным, иногда невозможным. Если возможно освободить уравнение от членов первой степени, то оно приводится к виду:

аналогичному уравнению (28). В этом случае каждой точке М(x, y, z) на поверхности отвечает также точка М′(-x, -y, -z), симметрич. первой относительно начала. Начало координат является центром симметрии поверхности, и она называется, поэтому, центральной. Если N не равно нулю, то, деля уравнение на N, мы приведем его к виду:

Здесь все три коэффициента не могут быть отрицательными, ибо тогда левая часть уравнения всегда имела бы отрицательное значение. Следовательно, либо все 3 коэффициента имеют положительные значения, либо между ними есть один отрицательный, либо 2 отрицательных. В первом случае уравнение приводится к виду:

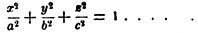
(39)

и выражает эллипсоид (фиг. 22). Это есть замкнутая поверхность, которая при пересечении плоскостью всегда дает в сечении эллипс. Оси координат служат осями симметрии поверхности; расположенные по этим осям диаметры имеют длины 2a, 2b, 2c; это суть так называемые оси эллипсоида. Если две из этих осей равны, то поверхность обращается в поверхность вращения, которая получается при вращении эллипса вокруг одной из своих осей.

Фиг. 22

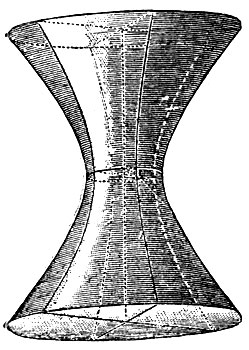
Если в уравнении (38) один из коэффициентов имеет отрицательное значение, то оно приводится к виду:

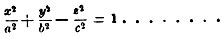
(40)

Оно выражает т. н. однополый гиперболоид (фиг. 23). Плоскости, перпендикулярные к оси z, пересекают эту поверхность по эллипсам, причем плоскость XY дает в сечении наименьший эллипс - горло гиперболоида. В сечении с плоскостями, проходящими через ось z, получаются гиперболы. Поверхность состоит из одной полости, простирающейся в бесконечность по обе стороны от горла.

Фиг. 23

Если в уравнении (38) имеется 2 отрицательных коэффициента, то оно приводится к виду:

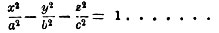
(41)

и выражает т.-н. двуполый гиперболоид (фиг. 24). При пересечении с плоскостями, перпендикулярным и к оси z-ов, он также дает эллипсы, а в сечении с плоскостями, проходящими через ось, - гиперболы. Но эта поверхность состоит из двух раздельных полостей, каждая из которых простирается в бесконечность.

Фиг. 24

Если в уравнении (38) один из коэффициентов, скажем, С, обращается в нуль, то оно выражает цилиндрическую поверхность, которую описывает прямая, параллельная оси z-ов и опирающаяся на коническое сечение,

В зависимости от того, будет ли это эллипс или гипербола, цилиндр называется эллиптическим или гиперболическим. Прямая, проходящая через центр направляющего конического сечения (42) параллельно образующей, называется осью цилиндрической поверхности. Так как поверхность простирается в бесконечность в обе стороны, то каждая точка на оси является центром симметрии поверхности. Она имеет, таким образом, бесчисленное множество центров.

Эллипсоид и два гиперболоида представляют собой важнейшие центральные поверхности 2-го порядка. Но в уравнении (37) свободный член N может оказаться нулем, тогда начало координат - центр симметрии поверхности - лежит на самой поверхности. Это - коническая поверхность о двух полах, как на фиг. 7; центром симметрии служит вершина конуса, а самая поверхность образуется прямой, которая движется, проходя постоянно через вершину и опираясь на кривую второго порядка. Эта поверхность является матерью конических сечений.

Таковы центральные поверхности второго порядка. Если уравнение (36) не может быть освобождено от членов, содержащих первые степени неизвестных т. е. не может быть приведено к виду (37), то поверхность вовсе не имеет центра. Исследование обнаруживает, однако, что в этом случае уравнение поверхности может быть приведено к такой форме, чтобы одна из координат входила только в первой степени; простейшая форма, в которой уравнение (36) может быть в этом случае представлено, имеет вид:

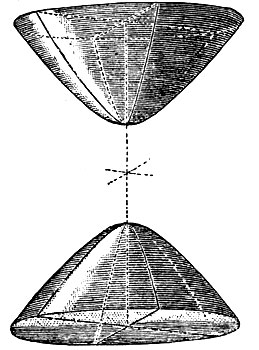
Все поверхности, выражаемые уравнениями этого вида, дают в сечении с плоскостями, проходящими через ось z-ов, параболы; они называются, поэтому, параболоидами. Если коэффициенты A и В имеют одинаковые знаки, то в сечении с плоскостями, перпендикуляр к оси z, поверхность дает эллипсы; такая поверхность называется эллиптическим параболоидом (фиг. 25). Если же коэффициенты A и В имеют противоположные знаки, то в сечении с перпендикулярными плоскостями получаются гиперболы; поверхность называется гиперболическим параболоидом (фиг. 26); на рисунках 25 и 26 изображены, конечно, лишь небольшие части поверхностей, простирающихся в бесконечность.

Фиг. 25

Фиг. 26

Таковы различные типы поверхностей второго порядка. Как мы видели выше, кривые второго порядка были открыты и изучены еще греками; аналитическая геометрия осветила лишь теорию этих замечательных кривых с иной точки зрения и дала новые пути к исследованию их. Напротив, поверхности 2-го порядка были открыты и расклассифицированы исключительно на основании аналитических соображений. Эйлеру, давшему в своем замечательном сочинении "Introductio in analysin infinitorum" (1748) аналитическую классификацию кривых второго порядка, принадлежит также классификация поверхностей 2-го порядка. Чисто геометрическая теория их была дана позже Штейнером(I. Steiner. "Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von einauder"; 1832).

Аналитическая геометрия ставит по отношению к поверхностям вопросы, совершенно аналогичные тем, которые составляют предмет аналитической теории кривых второго порядка. Наиболее важное свойство поверхностей второго порядка, с точки зрения Эйлера, заключается в том, что прямая пересекает их не более, чем в двух точках, а всякая плоскость сечет эти поверхности по коническому сечению. В связи с этим надо остановиться на следующем замечательном обстоятельстве. Мы знаем, что кривая второго порядка вырождается иногда в совокупность двух прямых. Сообразно этому и плоскость может иногда пересекать поверхность второго порядка по двум прямым - это имеет место, например, при пересечении конуса плоскостью, проходящей через вершину, и при пересечении цилиндра плоскостью, параллельной оси. Но замечательно, что и другие поверхности второго порядка могут давать иногда в пересечении с плоскостями две прямые. Этим свойством обладают однополый гиперболоид и гиперболический параболоид. Более того, через каждую точку той и другой поверхности можно провести плоскость, рассекающую поверхность по двум прямым. Иначе говоря, - через каждую точку поверхности проходят две прямые, расположенные целиком на этой поверхности. Вся поверхность, таким образом, покрывается двумя системами прямых; на поверхности этого рода можно смотреть, как на линейчатые поверхности, т. е. такие, которые образованы движением прямой. Простейшие виды линейчатых поверхностей хорошо известны в элементарной геометрии: это конические и цилиндрические поверхности. Но эти простейшие поверхности обладают следующей замечательной особенностью: любые две образующие их лежат в одной плоскости; поверхность образуется прямой, перемещающейся таким образом, что она постоянно пересекает предыдущее свое положение или остается ему параллельной. В тесной связи с этим стоит то обстоятельство, что поверхности этого рода могут быть, как говорят, развернуты на плоскость: мы представляем себе, что коническую и цилиндрическую поверхность можно разогнуть таким образом, чтобы она покрыла плоскость. Эти поверхности называются, поэтому, развертывающимися на плоскость. Иначе обстоит дело в однополом гиперболоиде и гиперболическом параболоиде. Эти поверхности, как уже сказано, также могут быть образованы движением прямой линии, но самое движение совершается иначе: каждая образующая не пересекает своего предыдущего положения; она не только отклоняется от него на небольшой угол, но в отходит от него на некоторое расстояние в другую плоскость. Так, например, гиперболический параболоид можно получить движением прямой следующим образом: представим себе некоторую плоскость и две неподвижные прямые АВ и A′В′, не лежащие в одной плоскости (фиг. 27). Положим, что третья прямая MN (образующая) движется таким образом, что она остается параллельной некоторой плоскости и в то же время постоянно пересекает обе неподвижные прямые - АВ и A′В′. Ясно, что при этих условиях последовательные положение прямой MN, даже сколь угодно близкие, располагают я в различных плоскостях. Этого рода поверхности не могут быть развернуты на плоскость; они называются косыми линейчатыми поверхностями.

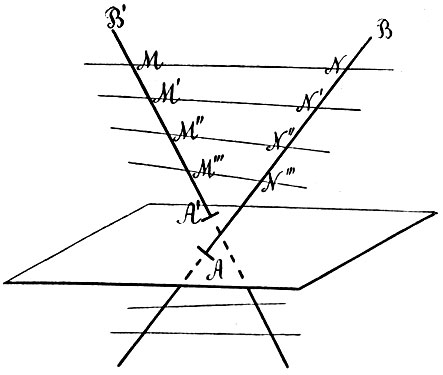
Фиг. 27

Возвратимся теперь к тому факту, что плоскость сечет поверхность второго порядка по кривой второго порядка. Пусть O будет точка, не лежащая на данной поверхности 2-го порядка. Проведем через точку O произвольную плоскость, пересекающую данную поверхность по коническому сечению P: точке O отвечает относительно этого конического сечения поляра р. Так как через точку O можно провести бесчисленное множество плоскостей, то ей отвечает бесчисленное множество поляр. Исследование обнаруживает, что они располагаются все в одной плоскости; эта плоскость называется полярной плоскостью точки O относительно конического сечения. Если из точки O можно провести к поверхности пучок касательных, то точки касания последних образуют коническое сечение, которое представляет собою пересечение поверхности с полярной плоскостью точки O. Если точка O лежит на поверхности, то полярная плоскость обращается в касательную плоскость к поверхности в этой точке. Соответствие между полюсом и полярной плоскостью, устанавливаемое поверхностью второго порядка, представляет собой новый вид геометрического соответствия, которое получает развитие в проективной геометрии.

Мы видим, таким образом, что в теории поверхностей второго порядка получают дальнейшее развитие те идеи, которые вложены в учение о кривых 2-го порядка. В общей теории алгебраических поверхностей эти идеи значительно усложняются. Если при исследовании кривых высших порядков на сцену выступают особенные точки, то здесь эти особенные точки образуют часто целые кривые на поверхности. По этим кривым либо пересекаются отдельные полости поверхности (линии кратных точек), либо сходятся отдельные части их (ребра поверхности), либо перегибаются части поверхности с одной стороны касательной плоскости на другую (лиши перегиба). Изучение этих особенностей и связанная с этим классификация алгебраических поверхностей высших порядков представляет большие затруднения; во многих своих частях это учение еще ждет исследователей.

VI. Дифференциальные методы в Геометрии.

Ровно через 100 лет после того, как появилась в свет "Геометрия" Декарта (1637-1736), был опубликован бессмертный мемуар Ньютона, "Метод флюксий", послуживший основой современного анализа бесконечно малых. Этот замечательный мемуар был написан еще в 1671 г. В ст. "Исчисление бесконечно малых" читатель найдет изложение эволюции, которой подверглись новые идеи от момента их зарождения до эпохи общего признания, в которой и относится опубликование мемуара после смерти его великого автора. Полное заглавие мемуара ("Methodus fluxionum et serierum in finitarum cum eiusdem applicatione ad curvarum geometriam") уже свидетельствует, что новое исчисление в первые же годы после своего зарождения получило применение к геометрии; более того, исчисление бесконечно малых в значительной мере обязано своим происхождением некоторым классическим геометрическим задачам, к которым мы сейчас обратимся. Когда же новый анализ развернулся, то внесение его идей в аналитическую геометрию послужило таким же мощным импульсом, как и появление основных идей Декарта и Ферма. Те исследования, о которых была речь в предыдущих двух отделах, носят чисто алгебраический характер; они имеют применение только к тем кривым и поверхностям, которые выражаются алгебраическим уравнением между координатами. Анализ бесконечно малых чужд этих ограничений; он находит себе применение в неизмеримо более широком комплексе функций; его творцам и основателям даже казалось, что он применим ко всем непрерывным функциям. Сообразно этому и методы приложения анализа бесконечно-малых к геометрии носят неизмеримо более общий характер, нежели те приемы, которыми получены результаты, изложенные в двух предыдущих отделах; они составляют дифференциальную геометрию. Здесь мы не находим классификации отдельных типов кривых; здесь мы имеем лишь такие исследования, которые применяются ко всякой кривой, выражаемой на плоскости уравнением вида

(в пространстве - двумя уравнениями такого рода), если только функция f(x) имеет первые две производные. Геометрическое происхождение понятия о производной с полною ясностью изложено в статье "Высшая математика" (XII, 84), аналитическое установление этого понятия читатель найдет в ст. "Исчисление бесконечно малых". Для понимания формул и вычислений дифференциальной геометрии необходимо вполне владеть этим понятием. Однако при изложении настоящего отдела мы сосредоточим внимание, главным образом, на геометрической стороне дела - на сущности задач и на результатах, к которым приводит их решение.

Все вопросы, которыми занимается дифференциальная Г., так или иначе сводятся к определению предельного положения того или иного образа по неограниченному ряду приближенных его положений. Точкой отправления здесь служит задача о касательной, классический вопрос, приведший к понятию о флюксии или производной.

Если проведем секущую к кривой через точку M и весьма близкую к ней точку M′ (фиг. 20 а), а затем станем точку М′ неограниченно приближать к М, то положение секущей будет меняться, но будет при этом неограниченно приближаться к некоторому предельному положению, которое и представляет собою касательную в точке М. Как разыскать эту касательную, как построить ее геометрически, как составить аналитически ее уравнение?

Если координаты точки М суть (а, b), то уравнение касательной, как и уравнение каждой прямой, через эту точку проходящей, имеет вид (20). Весь вопрос заключается в определении коэффициента k, так называемого углового коэффициента касательной, т. е. тангенса угла, который она образует с осью абсцисс. Этот угловой коэффициент и представляет собой геометрическое определение производной от функции f(x), представляющей правую часть уравнения (44). Аналитически образование производной в связи с задачей о касательной выяснено в указанном выше месте статьи "Высш. математика". Правила образования производной от данной функции дает дифференциальное исчисление. В пору первого развития исчисления бесконечно малых полагали, что всякая непрерывная функция имеет производную при каждом значении независимой переменной, а потому каждая непрерывная кривая имеет касательную в каждой своей точке. Однако, глубокие исследования ХIХ столетия разрушили эту иллюзию и этим, конечно, несколько сузили комплекс образов, к которым применяется дифференциальная геометрия. Дальнейшие наши рассуждения относятся только к таким кривым вида (44), для которых левая часть уравнения имеет первую и вторую производные. Из того, что мы выражаем кривую уравнением вида (44), следует, что мы имеем в виду плоскую кривую, т. е. расположенную в одной плоскости. О более сложных кривых речь еще впереди. Производная от функции f(x) обозначается через f′(x); и сообразно этому уравнение касательной к плоской кривой (44) в точке (а, b) имеет вид:

Прямая, проведенная через точку кривой перпендикулярно к касательной в этой точке, называется нормалью к кривой. Главное значение касательной и нормали в прикладной математике заключается в следующем: если некоторая точка движется по кривой, то скорость этого движения в каждый момент направлена по касательной к траектории в той точке, в которой в этот момент находится движущаяся точка. Если же движется неизменяемая фигура, некоторая точка которой описывает данную кривую, то так называемый мгновенный центр движения в каждый момент лежит на нормали к кривой. Шаль (Chasles), Роберваль (Roberval) и др. основали на этом свои приемы для геометрического построения касательной нормали к кривой. Эти приемы находят себе применение всякий раз, как удается указать такой способ образования кривой при помощи движения, который дает возможность непосредственно определить либо направление скорости, либо положение мгновенного центра движения.

Пусть М будет некоторая точка на данной кривой, MN - нормаль к кривой в этой точке. Возьмем точку М′, весьма близкую к М (фиг. 28), и в ней проведем нормаль M′N′. Эта нормаль пересечет предыдущую в некоторой точке C′. Если теперь мы будем приближать точку М′ к М, то положение точки пересечения C′ будет, как оказывается, неограниченно приближаться к некоторому предельному положению - к некоторой точке C на исходной нормали MN. Эта точка C называется центром кривизны кривой, соответствующим ее точке М; расстояние МС называется радиусом кривизны кривой в точке М; окружность, описанная из точки C радиусом СМ - окружностью кривизны в точке M.

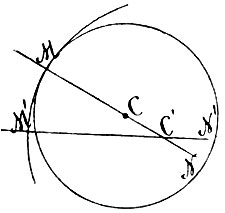
Фиг. 28

Это суть основные понятия дифференциальной геометрии. Если исходной кривой служит окружность, то центр кривизны всегда занимает одно и то же положение - он совпадает с центром окружности; радиус кривизны совпадает с радиусом окружности. Чем меньше радиус окружности, тем быстрее она загибается, искривляется и, наоборот, чем больше радиус окружности, тем меньше небольшая дуга ее отличается от прямой, тем меньше ее кривизна. Сообразно этому, за меру кривизны окружности принимается величина, обратная ее радиусу за меру же кривизны в данной точке любой кривой принимается величина, обратная радиусу кривизны в этой точке. Значение окружности кривизны в данной точке кривой заключается в том, что это есть окружность, имеющая с нею в данной точке кривой наиболее тесное соприкосновение. Во многих случаях дуга кривой в ближайших частях точки М может быть заменена дугой окружности кривизны в этой точке. Так, например, если точка движется по окружности и имеет в данный момент скорость v, то так называемое центростремительное ускорение этого движения направлено к центру окружности и равно v²/r. Если движение совершается по любой кривой, то центростремительное ускорение направлено к центру кривизны и также выражается формулой v²/r , где r - радиус кривизны в данной точке кривой. Движение по кривой вблизи точки М как бы заменяется движением по окружности кривизны в этой точке. Бресс (Bresse) в другие пользуются этим обстоятельством для геометрического построения центра кривизны в каждой точке кривой.

К идее о кривизне кривой можно прийти и иным путем. Обозначим через α угол между нормалями MN и M′N′; этот угол выражает уклонение нормали на протяжении дуги MM′ (или уклонение касательной на этом протяжении, так как угол между нормалями равен углу между касательными). Отношение выражает как бы скорость отклонения нормали или касательной вдоль дуги MM′; предел этого отношения, когда точка M′ стремится к M, и представляет собой кривизну в этой точке. Кривизна прямой постоянно равна нулю, ибо касательная и нормаль здесь вовсе не отклоняются. В окружности кривизна имеет одинаковое значение во всех ее точках. Прямая и окружность суть линии, имеющие постоянную кривизну; во всех других кривых кривизна меняется от точки к точке.

Как мы уже указали, в случае окружности центр кривизны всегда лежит в одной и той же точке - в центре ее. В других кривых положение центра окружности меняется от точки к точке. Если мы для каждой точки кривой построим ее центр кривизны N (фиг. 29), то геометрическое место точек N составит новую кривую - ее эволюту или развертку. Самая же кривая по отношению к своей эволюте называется эвольвентой или разверзающей кривой. Между точками эвольвенты и эволюты устанавливается таким образом геометрическое соответствие. Каждой точке М эвольвенты отвечает ее центр кривизны - точка N на эволюте; и, так как центр кривизны лежит всегда на нормали к кривой, то каждая точка эволюты лежит на нормали соответствующей точки эвольвенты. Но замечательно, что эта нормаль в то же время касается эвольвенты: нормали к эвольвенте служат касательными к эволюте; эволюта как бы огибает пучок нормалей. Мало того, если мы возьмем две точки эвольвенты М и М′ (фиг. 29) и соответствующие точки N и N′ на эволюте, то разность между радиусами кривизны МN и М′N′ как раз равна длине эволюты NN' на этом протяжении: длина радиуса кривизны эвольвенты нарастает как раз на длину дуги соответствующей части эволюты. Если бы мы в некоторой точке N эволюты закрепили нить и направили ее по касательной к кривой до точки M, затем, постоянно натягивая нить, вели бы ее так, чтобы точка М все время оставалась на эвольвенте, то нить постоянно облегала бы эволюту. Укажем еще следующее замечательное обстоятельство в соответствии между эвольвентой и эволютой: каждой эвольвенте отвечает одна определенная эволюта; но каждой эволюте отвечает бесчисленное множество эвольвент. Это значить: если дана кривая, то мы имеем возможность построить множество кривых, для которых данная кривая служит эволютой.

Фиг. 29

В этом рассуждении мы в первый раз встречаемся с семейством линий. Этим семейством здесь является совокупность нормалей к эвольвенте или совокупность касательных к эволюте. Понятие о семействе кривых играет весьма важную роль в геометрии. В наиболее простом случае семейство кривых выражается уравнением вида:

где α есть переменная, как говорят, параметр, значение которого совершенно не зависит от значения координат. Если мы дадим параметру α определенное численное значение, то уравнение (46) тотчас примет обычную форму f(x, у)=0, т. е. выразить некоторую кривую на плоскости. Каждому значению параметра α отвечает, таким образом, определенная кривая; совокупность этих кривых и образует семейство кривых.

В дальнейшем мы будем иметь в виду исключительно семейства кривых этого рода, т. е. зависящие от одного параметра. Такое семейство представляет собой совокупность концентрических окружностей (отличающихся одна от другой, следовательно, только значением радиуса), совокупность софокусных эллипсов (т. е. имеющих общие фокусы и отличающихся только эксцентриситетом) и т. п. На фиг. 30 между двумя жирными окружностями изображена окружность радиуса R; из каждой точки этой окружности описана окружность меньшего, но постоянного радиуса r; совокупность этих малых окружностей образ. семейство кривых.

Фиг. 30

Если мы возьмем две, как говорят, смежные кривые семейства, т. е. две весьма близкие кривые (параметры которых между собой весьма мало отличаются), то они обыкновенно пересекаются в одной или нескольких точках. Так, например, окружности C и C′ на фиг. 30 пересекаются в точках P′ и Q′. Если теперь, сохраняя неподвижной одну из этих двух кривых, будем неограниченно приближать семейства, то эти точки к ней другую кривую семейства, то эти точки пересечения обыкновенно неограниченно приближаются к некоторым неопределенным предельным положениям. Так, например, когда окружность С′ неограниченно приближается к С, то точки P′ и Q′ стремятся к предельному положению P и Q. Таким образом, на каждой кривой семейства получаются определенные точки, представляющие предельные положения точек их пересечения со смежными кривыми. Геометрическое место этих точек представляет собой огибающую данного семейства кривых. Для семейства, изображенного на фиг. 30, огибающая состоит из двух окружностей радиусов R+r и R-r. Как мы видим на чертеже, эта огибающая касается всех окружностей огибаемого семейства. Это явление общее: огибающая всегда касается в общей точке той из огибаемых, которую она в этой точке встречает. Эволюта, как мы уже упомянули выше, есть не что иное, как огибающая семейства нормалей в эвольвенте. Учение об огибающих играет значительную роль в прикладной математике, в особенности в механике, в учении о зацеплениях.

Мы полагаем, что мы в достаточной мере выяснили характер тех задач, связанных с предельным переходом, которые решаются дифференциальными методами в применении к плоским кривым. Исчерпать же этот материал здесь все равно невозможно. Мы, переходим, поэтому, к кривым двоякой кривизны и здесь мы будем еще кратче.

Кривая называется кривой двоякой кривизны, если никакая часть ее не умещается целиком в одной плоскости. Самым простым примером такой кривой является так называемая винтовая линия. Если мы возьмем прямоугольный треугольник и обвернем его вокруг круглого цилиндра так, чтобы один из катетов обогнул основание, то гипотенуза свернется в кривую двоякой кривизны, называемую винтовой линией (фиг. 31).

Фиг. 31

Касательная определяется на кривой двоякой кривизны совершенно так же, как и на плоской кривой, т. е., как предельное положение секущей. Но так как эти кривые мы рассматриваем не в плоскости, а в пространстве, то перпендикуляров к касательной в данной ее точке, или нормалей к кривой, можно провести бесчисленное множество. Как перпендикуляры к одной и той же прямой в одной точке, эти нормали образуют плоскость - нормальную плоскость к кривой в данной ее точке. На фиг. 32 изображена кривая двоякой кривизны, касательная МК к ней в точке М и нормальная плоскость RS.

Фиг. 32

Если мы теперь представим себе какую-либо плоскость, проходящую через касательную, и станем ее вращать вокруг касательной, то глазу ясно, что она близ точки М будет приходить с кривой то в более, то в менее тесное соприкосновение. При каком положении это соприкосновение сделается наиболее тесным? Этот вопрос разрешается следующим образом. Возьмем вблизи точки М на кривой две другие точки М′ и М″ и через 3 точки М, М′, М″ проведем плоскость. Если мы станем сближать точки М′ и М″ с М, то плоскость будет приближаться к некоторому предельному положению; так как в этом предельном положении прямые ММ′ и ММ" сольются с касательной, то предельная плоскость будет проходить через касательную; она и представляет плоскость наиболее тесного соприкосновения - так называемую соприкасающуюся плоскость в точке M; на фиг. 32 это есть плоскость PQ. Нормаль ML к кривой в точке М, проведенная в соприкасающейся плоскости, называется главной нормалью к кривой в этой точке. Главная нормаль представляет собой пересечение соприкасающейся плоскости с нормальной плоскостью. Наконец, прямая MN, перпендикулярная как к касательной, так и к главной нормали, называется бинормалью к кривой в этой точке.

Центр кривизны кривой двоякой кривизны не может быть определен так, как это было сделано для плоской кривой: главная нормаль к кривой может со смежной главной нормалью вовсе не пересекаться. Здесь нужно исходить из другой аналогии. Пусть МК будет касательная в точке М кривой, M′К′ касательная в смежной точке М′. Если α есть угол между этими прямыми, т. е. угол, на который отклоняется касательная при переходе от точки М к М′, то отношение α:ММ′, как и в случае плоской кривой, в известном смысле характеризует скорость ее искривления. Когда точка М′ неограниченно приближается к M, это отношение стремится к определенному пределу; это и есть кривизна кривой в точке М; обратная величина называется радиусом кривизны в этой точке. Выражаемый этим числом в тех же единицах, в которых выражается длина дуги MM′, отрезок откладывается по главной нормали в ту сторону, в которую загибается кривая; конечная точка этого отрезка и будет центром кривизны кривой.

На угол α можно смотреть также, как на отклонение нормальной плоскости при переходе от точки М к точке М′, ибо угол между нормальными плоскостями равен углу между касательными. Если мы обозначим через β угол, на который отклоняется соприкасающаяся плоскость при переходе от точки М к М′, то отношение β:ММ′ также стремится к определенному пределу, когда точка М′ приближается к М; этот предел называют второй кривизной кривой в точке М. Первая кривизна характеризует загибание кривой от нормальной плоскости, а вторая - от соприкасающейся плоскости.

Если кривая плоская, то все ее касательные расположены в той же плоскости; но если это кривая двоякой кривизны, то совокупность ее касательных образует линейчатую поверхность и притом развертывающуюся на плоскость. Это наиболее общий тип развертывающихся линейчатых поверхностей в том смысле, что каждая развертывающаяся на плоскость линейчатая поверхность может быть рассматриваема, как геометрическое место касательных к некоторой кривой двоякой кривизны; эта кривая называется ребром возврата поверхности. В конических поверхностях ребро возврата вырождается в точку, в цилиндрических - даже в бесконечно удаленную точку.

Мы естественно пришли, таким образом, к поверхностям. Через каждую точку М на поверхности проходит бесчисленное множество кривых, а к каждой кривой можно провести касательную. Геометрическое место этих касательных, как оказывается, есть плоскость; она называется касательной плоскостью к поверхности в данной точке кривой. Обыкновенно представляют себе, что касательная плоскость к поверхности в точке M, по крайней мере, вблизи этой точки других общих точек с поверхностью не имеет; но это не так. В эллипсоиде, например, это действительно так имеете место; но в однополом гиперболоиде, скажем, или в гиперболическом параболоиде дело обстоит совершенно иначе: здесь касательная плоскость рассекает поверхность всегда по двум образующим и даже вблизи точки касания поверхность всегда располагается по обе стороны касательной плоскости. Руководясь этим частным случаем, точку на поверхности называют эллиптической, если вблизи этой точки поверхность располагается по одну сторону касательной плоскости, и гиперболической - когда она располагается по обе стороны касательной плоскости. Если рассечь поверхность плоскостью, весьма близкой к касательной плоскости и параллельной ей, то это сечение вблизи эллиптической точки будет весьма приближаться к небольшому эллипсу, а вблизи гиперболической точки - к небольшой части гиперболы. Среднее место занимают параболические точки, вблизи которых сечение уподобляется части параболы. В параболической точке касательная плоскость иногда рассекает поверхность, иногда не рассекает ее. Это несколько расходится с приведенным выше определением эллиптической и гиперболической точки: но более точное различение основано на аналитических критериях, которых мы не можем здесь приводить.

Прямая, перпендикулярная к касательной плоскости в точке касания M, называется нормалью к поверхности в этой точке. Если мы через нормаль проведем какую либо плоскость (фиг. 33), то она пересечет поверхность по кривой, которую называют нормальным сечением поверхности, таких нормальных сечений через данную точку на поверхности можно, очевидно, провести бесчисленное множество. Каждое нормальное сечение имеет в точке М определенную кривизну и определенный центр кривизны; последний всегда расположен па нормали MN к поверхности. Однако, в этом отношении возможно двоякое положение. Если касательная плоскость в точке М не рассекает поверхности, то все сечения расположены по одну сторону касательной плоскости, и с той же стороны располагаются по нормали их центры кривизны. В этом случае, следуя Гауссу, говорят, что кривизна всех нормальных сечений имеет одинаковый знак; даже, более определенно, говорят, что все сечения имеют положительную кривизну. Если же касательная плоскость рассекает поверхность, то центры кривизны одних нормальных сечений лежат на нормали по одну сторону касательной плоскости, а на других - по другую. В этом случае кривизнам сечений, имеющих центры по разные стороны касательной плоскости, приписываются различные знаки. С какой стороны считать кривизну положительной, а с какой отрицательной, совершенно безразлично; но коль скоро это установлено, каждое нормальное сечение приобретает кривизну, определенную по величине и по знаку. Если мы проследим за ходом изменения кривизны в нормальных сечениях, то окажется, что в обыкновенных точках поверхности имеются два взаимно перпендикулярных нормальных сечения, в одном из которых кривизна достигает максимума, а в другом минимума (принимая при этом, конечно, во внимание и знаки кривизн). Эти два сечения называются главными сечениями поверхности, а произведение их кривизн называется кривизной самой поверхности в точке M. Таким образом, поверхность имеет в данной точке положительную кривизну, если касательная плоскость не пересекает поверхности (ибо в этом случае кривизны главных сечений имеют одинаковые знаки), и отрицательную кривизну, если кас. плоскость в этой точке рассекает поверхность. Эллипсоид, однополый гиперболоид и эллиптический параболоид имеют положительную кривизну во всех своих точках, а однополый гиперболоид и гиперболический параболоид имеюсь в каждой точке отрицательную кривизну. Но от точки к точке на эллипсоиде, скажем, кривизна по абсолютной величине меняется. Есть, однако, поверхности, которые имеют во всех своих точка одну и ту же положительную кривизну. Самая простая из таких поверхностей постоянной положительной кривизны есть шаровая поверхность (сфера). Чтоб составить себе представление о других поверхностях, имеющих во всех своих точках постоянную положительную кривизну, нужно исходить из знаменитой теоремы Гаусса, доказанной в замечательном мемуаре "Disquisitiones generales circa superficies curves". Она заключается в следующем: если мы возьмем кусок поверхности и, представляя себе таковую, как бесконечно тонкую пленку, станем ее непрерывно деформировать, не делая никаких разрывов или складок, т. е. просто будем ее изгибать, как тонкий кусок материи, то кривизна в каждой точке поверхности будет оставаться без изменения. Если мы, поэтому, вырежем кусок сферы и как-нибудь его изогнем, то мы получим поверхность постоянной положительной кривизны. Особенно характерна следующая форма: возьмем сферу и через два противоположных ее полюса проведем два меридиана (две полуокружности). Сделав по этим меридианам разрез, мы получим сферический вырезок; сводя его концы, образуем нечто вроде челнока - обычная форма поверхностей постоянной положительной кривизны. Но существуют также поверхности постоянной отрицательной кривизны. По их аналогии в этом отношении со сферой, Бельтрами назвал их псевдосферами. Различные формы псевдосферы необычайно разнообразны. Подобно тому, как сфера есть поверхность вращения постоянной положительной кривизны, имеются поверхности вращения постоянной отрицательной кривизны; они имеют форму неограниченно суживающегося бокала, как это изображено на фиг. 34.

Фиг. 33

Фиг. 34

Разработка начал дифференциального исследования кривых линий и поверхностей относится, главным образом к XVIII столетию. Во главе большой группы геометров, занятых их разработкой, стоят Клеро (Clairaut, "Traité des courbes à double courbure") и Эйлер ("Introductio in analysin infinitorum", 1748). По мере развития анализа бесконечно малых углубляются, конечно, и его приложения к геометрии, выдвигается ряд задач, решение которых зависит от наиболее сложных аналитических форм - от дифференциальных уравнений; а обратно, геометрические соображения становятся руководящей нитью в деле исследования (интегрирования) этих уравнений. В этой области идей исходную руководящую роль играют работы Монжа (G. Monge, главным образом "Application de l'analyse a la géométrie" с 1795 г.), с именем которого нам еще ниже придется встретиться. Однако, эти идеи связаны такими глубокими аналитическими соображениями, что они могут найти себе место лишь в последнем отделе статьи "Исчисление бесконечно малых".

VII. Трансцендентные кривые и поверхности.

Как мы уже указали выше, дифференциальные методы имеют то преимущество перед алгебраическими кривыми, что они находят себе применение не только к алгебраическим, но и к трансцендентным кривым и поверхностям. Этим последним образам мы уделим теперь несколько слов, чтобы познакомить с наиболее важными кривыми и поверхностями этого рода.

При необычайном разнообразии, которое могут представлять трансцендентные кривые, они, можно сказать, вовсе не поддаются классификации. Здесь может быть речь скорее только о группировке этого рода кривых, независимо одна от другой появляющихся то в теоретических, то в прикладных исследованиях.

Очень большая категория плоских трансцендентных кривых относится к числу рулет. Под этим разумеют кривые, которые получаются следующим образом. Представим себе, что некоторая неизменяемая плоская фигура движется таким образом, что некоторая ее кривая катится без скольжения по другой, неподвижной кривой. На фиг. 35 изображена неподвижная окружность С, по которой катится круг М; этот круг может, конечно, составлять часть большей плоской фигуры, движущейся вместе с ним. Путь, описываемый любою точкой движущейся таким образом фигуры, называется рулетой. При чрезвычайном разнообразии, которое могут представлять неподвижная кривая и катящиеся по ней линии, формы рулет беспредельно разнообразны. Де-ла-Гир показал даже, что всякая плоская кривая может быть рассматриваема, как рулета. Если как подвижная, так и неподвижная кривая представляют собой окружности, то рулета называется трохоидой, и именно эпитрохоидой - когда подвижный круг лежит вне неподвижного, и гипотрохоидой - когда подвижный круг лежит внутри неподвижного. На фиг. 35а изображена эпитрохоида РР′ на фиг. 35b - гипотрохоида РР′. Трохоида не всегда представляет собой трансцендентную кривую: если отношение радиусов двух кругов есть число рациональное, то трохоида оказывается алгебраической кривой: если оно иррациональное, то трохоида есть трансцендентная кривая. Если неподвижная окружность вырождается в прямую, то трохоида называется циклоидой. Итак, циклоида есть кривая, которую описывает точка неизменяемой фигуры, неразрывно связанной с окружностью, катящейся по прямой. На фиг. 36 изображена циклоида, которую описывает внутренняя точка круга. Рулеты играют очень важную роль в механике, так как всякое движение в плоскости может быть сведено к качению рулет.

Фиг. 35a

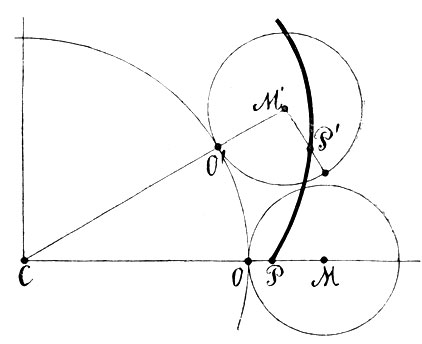
Фиг. 35b

Фиг. 36

Из спиралей укажем так называемую Архимедову спираль (фиг, 37), которая выражается в полярных координатах уравнения r=αυ, синусоидальную спираль, которая имеет уравнение вида rⁿ=aⁿsinυ, и логарифмические спирали, которые выражаются уравнением r=αeυ. Все эти кривые бесчисленное множество раз завиваются вокруг начала координат и отличаются между собой лишь скоростью нарастания радиуса-вектора, т. е. расстояния точки от начал по мере загибания кривой.

Фиг. 37

В математической физике огромную роль играют так называемые синусоиды, по которым происходят гармонические колебания точки в звуковой волне. Схематически этими кривыми изображаются также поперечные колебания в световой и электрической волне. Синусоида в декартовых координатах выражается уравнением:

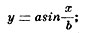
она изображена на черт. 38.

Фиг. 38

Историческое значение имеет квадратрикса (фиг. 39), уравнение которой имеет вид:

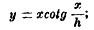
и цепная линия (фиг. 40), напоминающая параболу и выражаемая уравнением

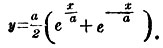
Фиг. 39

Фиг. 40

Квадратриксой еще в древности пользовались для квадратуры круга (см.), а по цепной линии свешивается тяжелая нить, подвешенная в двух точках.

Из трансцендентных кривых двоякой кривизны укажем упомянутую уже винтовую линию, замечательную в том отношении, что она во всех своих точках имеет постоянную как первую, так и вторую кривизну, и локсодромы, т. е. кривые, которые на поверхности вращения изгибаются таким образом, что во всех своих точках образуют один и тот же угол с меридианом.

Из трансцендентных поверхностей мы укажем только винтовую поверхность, которая образуется прямой линией, движущейся параллельно основанию круглого цилиндра, на который намотана винтовая линия, и в своем движении постоянно опирается на винтовую линию и ось цилиндра. Это есть косая линейчатая поверхность.

VIII. Проективная геометрия.

Хотя предыдущий очерк охватывает лишь начальные элементы современной аналитической и дифференциальной геометрии, мы полагаем, что он дает все-таки некоторое представление о том огромном развитии, которое получила геометрия под влиянием идей Декарта, Ферма, Лейбница и Ньютона. Глав. ценность аналитического метода заключается в его необычайно широкой общности; Декарту не даром приписывают фразу: "Я разрешил все задачи геометрии" Но, как всякий прием в науке, так и аналитически метод геометрии имеет и свою оборотную сторону. Широкая общность часто покупается ценой очень сложных аналитических рассуждений, и там, где счастливый геометрический прием иногда удачно справляется с вопросом в нескольких штрихах, аналист бывает поставлен в необходимость с трудом расчищать путь сложных, иногда даже мало осуществимых вычислений. Вот почему среди математиков всегда оставались приверженцы чисто геометрических методов, для которых девизом служило требование: "geometria geometrice"; это значит - геометрию надо строить геометрически, без чуждых ей арифметических и алгебраических средств. Этого не нужно понимать в том смысле, что кто-либо из крупных математиков был склонен отрицать значение аналитических методов в геометрии; но многие по складу своего ума предпочитали синтетические приемы и утверждали, что там, где чисто геометрические методы находят себе приложение, они приводят к цели быстрее и изящнее, они больше отвечают духу геометрии. Таким образом, чистая геометрия сохранила своих сторонников, ставивших себе задачей обработать синтетически тот материал, который выдвинула аналитическая геометрия. В этой широкой постановке задача, однако, не получила разрешения. Хотя Штейнеру и удавалось справляться средствами классической геометрии с труднейшими задачами вариационного исчисления, но эти работы остались изолированными, так сказать, случайными. Но сторонники чистой геометрии сумели выделить дисциплину, которая не только исчерпывается синтетическими методами, но вовсе не нуждается в понятии о числе и о величине, - дисциплину, в которой принцип "geometria geometrice" проведен до крайних пределов. Развитие этой дисциплины относится к концу XVIII и началу XIX столетия, а творцами ее должны быть признаны два французских математика - Понсле (Poncelet) и Шаль (Chasles) и два немецких - Мёбиус (Möbius) и Штейнер (Steiner); в руках Штаудта (v. Staudt) и Рейе (Reye) она получила свое завершение. По преобладанию в ней метода проектирования она получила название "проективной геометрии"; но принятое позже название "геометрии положения" (Geometrie der Lage) более соответствует содержанию дисциплины. В современном своем развитии она владеет средствами, во многих частях заменяющими методы аналитической геометрии; она послужила руководящей нитью для развития так называемой "новой алгебры".

Геометрия, которая ставит себе задачей не оперировать вовсе над величинами, естественно, должна быть чужда всякой метрики; материалом проективной геометрии являются, поэтому, вопросы расположения, инцидентности и геометрического соответствия, насколько оно устанавливается геометрическими средствами (см. отдел I, в частности рубрику 4). В указанном здесь месте отдела 1-го был уже приведен пример такого рода соответствия - так называемая перспектива. Этот прием играет в проективной геометрии наиболее важную роль; мы вынуждены, поэтому, к нему возвратиться.

Пусть O будет некоторая постоянная точка, S некоторый геометрический образ (линия, плоскость, другая поверхность), M произвольная точка. Если прямая ОМ встречает образ S в одной точке М′, то эта точка называется проекцией точки M на образ S из центра O. Если мы возьмем в одной плоскости две прямые MNPQ.... и M′N′P′Q′.... (фиг. 41), то мы можем каждую точку первой прямой проектировать из любого центра O, расположенного в той же плоскости, на вторую прямую. Таким образом, каждой точке первой прямой устанавливается соответствующая точка второй прямой; это соответствие называется перспективой. Устанавливая это соответствие, мы смотрим на каждую прямую, как на ряд точек, и каждой точке одного ряда относим точку другого ряда и обратно. Перспектива сводится к тому, что прямые ММ′, NN′, PP′, QQ′...., соединяющие соответственные точки, сходятся в одной точке О, в центре проекции.

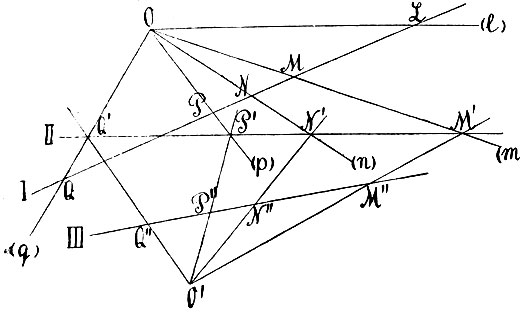
Фиг. 41

Совершенно аналогично тому, как здесь установлено перспект. соответствие между точками двух прямых, может быть установлено также соответствие между двумя плоскостями; это и сделано в рубр. 4 отдела 1-го. Перспектива занимала геометров очень давно в связи с вопросами, которым посвящен отдел X (см. ниже).

Уже в XVII столетии французский математик и архитектор Дезарг опубликовал впервые трактат о перспективе (G. Desargues, "Traité de la section perspective", 1636), оказавший большое влияние на развитие идей Попсле и Шаля. Но два обстоятельства играют особенно важную роль.

При систематическом развитии перспективы нельзя было, конечно, игнорировать того факта, что при перспективном соответствии двух прямых на каждой прямой есть точка, которой не отвечает точка другой прямой. На фиг. 41 точке L, лежащей в пересечении прямой OL (параллельной прямой II), с пр. I, не отвечает точка на пр. II, ибо проектирующий луч OL последней не встречает. Это простое обстоятельство играет необычайно важную роль в систематическом развитии учения о перспективе. Чтобы выйти из возникающ. отсюда затруднения, Дезарг вводит понятие о бесконечно-удаленных точках; именно, он смотрит на две параллельные прямые, как на пересекающиеся в бесконечно-удаленной точке; совокупность всех бесконечно-удаленных точек плоскости образует бесконечно-удаленную прямую, две параллельные плоскости пересекаются по бесконечно-удаленной прямой. По введении этих понятий любые две прямые на плоскости пересекаются: непараллельные в конечной точке, параллельные - в бесконечно-удаленной. Точно так же всегда пересекаются две плоскости по конечной идя по бесконечно-удаленной прямой. Но наглядно, конкретно эти бесконечно-удаленные образы трудно, а может быть даже и невозможно, себе представить. Вопрос о том, в какой мере допустимо введение этих идеальных образов, вызывал большие споры. Как и многие другие геометрические идеи, они были введены полубессознательно, с ними более мирились, чем признавали. Лишь в самое последнее время Клейн, Шур и другие вполне выяснили, почему эти идеальные образы не могут вести к противоречию; эти рассуждения, однако, слишком сложны, чтобы мы могли уделить им здесь место. Итак, с введением бесконечно-удаленных элементов каждой точке двух перспективных прямых отвечает точка на другой: точке L на прямой I (фиг. 41) отвечает бесконечно-удаленная точка прямой II.

Второе обстоятельство - вторая заслуга Дезарга - заключается в следующем: рассматривая 2 перспективных треугольника MNP и М′N′P′ (т. е. 2 треугольника, расположенные таким образом, что прямые ММ′, NN′, РР′ (фиг. 42) сходятся в одной точке О - центре перспективы), Дезарг обнаружил, что точки пересечения соответственных сторон этих треугольников (точка p - пересечение сторон MN и M′N′, точка m - пересечение прямых NP и N′P′ и точка n - пересечение прямых MP и М′Р′) расположены на одной прямой. Обратно, если 2 треугольника расположены таким образом, что точки пересечения соответственных сторон лежат на одной прямой, то эти треугольники перспективны, т. е. прямые, соединяющие соответственные вершины, сходятся в одной точке. Это предложение должно быть признано первой основной теоремой проективной геометрии. Ее роль будет выяснена ниже, но самая теорема уже представляет собой характерный пример предложения, относящегося к геометрии положения, т. е. совершенно чуждого всякой метрики. Однако, своей современной чистоты проективная геометрия достигла не сразу. Одно из основных понятий, играющих доминирующую роль в проективной геометрии, вводится у Шаля и Мёбиуса на основании метрических соображений, от которых проективную геометрию освободил только Штаудт. Мы будем следовать историческому развитию идей и, сообразно этому, начнем с метрического установления этого понятия.

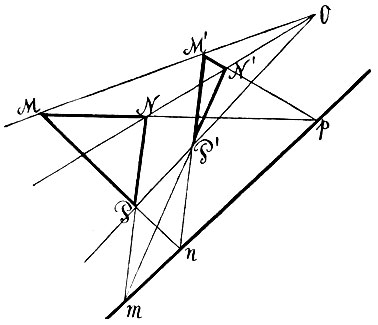
Фиг. 42

Если точки М, N, Р (фиг. 41) лежат на одной прямой, то говорят, что точка N делит отрезок MP в отношении 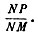При этом отрезки NP и NM отсчитываются по величине и по знаку, т. е. считаются положительными в одном направлении прямой и отрицательными в другом направлении. Когда точка N, как на фиг. 41, расположена между точками М и P, то отрезки NM и NP направлены в разные стороны, т. е. имеют противоположные знаки, и предыдущее отношение имеет отрицательное значение. Если же точка лежит вне отрезка РМ, как, напр., точка L на фиг. 41, то отрезки LP и LM направлены в одну сторону и имеют одинаковые знаки; отношение 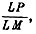в котором точка L делит отрезок РМ, имеет положительное значение.

Если точки P, М, N, L расположены на одной прямой, то частное тех отношений, в которых вторые две точки делят расстояние РМ, т. е.

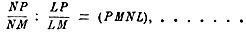
(45)

называется двойным или ангармоническим отношением четырех точек P, М, N, L и обозначается символом (PMNL), как это уже отмечено в равенстве (45).

Самые элементарные свойства треугольников, опирающихся на отрезки NP, NM и LP и LM и имеющих вершины в точке O, обнаруживают, что

(46)

если учитывать знаки углов так же, как и знаки отрезков. Для краткости обозначим через p, m, n, l лучи ОР, ОМ, ON, 0L, а через (np), (nm), (lp), (lm) будем обозначать углы NOP, NOM, LOP, LOM. Тогда правая часть равенства (46) будет построена совершенно аналогично левой; она называется двойным или ангармоническим отношением четырех лучей p, m, n, l, выходящих из общей точки O или, как говорят, принадлежащих одному пучку:

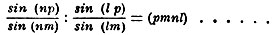
(47)

Предыдущее же соотношение (46) устанавливает следующее основное положение: если мы рассечем пучок лучей прямой линией, то ангармоническое отношение четырех точек на этой прямой всегда равно ангармоническому отношению четырех лучей, проходящих через эти точки.

Положим теперь, что мы имеем два перспективных ряда точек I и II. Тогда ангармоническое отношение точек (PMNL) равно ангармоническому отношению лучей (pmnl). Но точно так же ангармоническое отношение точек (P′M′N′L′) равно ангармоническому отношению тех же лучей (pmnl). Следовательно

Мы приходим, таким образом, к следующему основному предложению: если два ряда точек связаны перспективным соответствием, то ангармоническое отношение любых четырех точек одного ряда всегда равно ангармоническому отношению соответствующих четырех точек второго ряда.

Но это соотношение может иметь место и без того, чтобы два ряда точек были связаны перспективой. Представим себе третий ряд точек L″, М″, N″, P″, перспективный относительно второго, но при ином центре проекции O' (фиг. 41). В таком случае этот третий ряд, вообще говоря, не будет расположен перспективно относительно первого, т. е. прямые LL″, MM″, NN″, РР″, .... соединяющие соответствующие точки первого и третьего ряда, не будут проходить через общую точку. Между тем, соотношение, аналогичное соотношению (47), будет иметь место:

ибо каждое из этих двух ангармонических отношений равно (P′M′N′L′). Ряды I и III называются проективными. Вообще, если два ряда точек связаны геометрическим соответствием таким образом, что ангармоническое соотношение четырех точек всегда равно ангармоническому отношению четырех других точек, то эти ряды называются проективными. Перспектива представляет частный случай проективного соответствия. Ряды I и III на фиг. 41-ой, как было выяснено, представляют пример проективного, но не перспективного соответствия; однако, оно осуществлено при помощи двух перспектив. Вот эта последняя сторона дела представляет собой общее свойство проективного соответствия двух рядов точек: оно всегда может быть установлено при помощи нескольких перспектив при различных центрах.

Совершенно таким же образом устанавливается проективное соответствие между двумя пучками лучей. Как вскользь уже было упомянуто, под пучком лучей разумеют совокупность прямых, расположенных в одной плоскости и проходящих через общую точку. Если нам дано 2 пучка, то мы можем установить между ними соответствие таким образом, чтобы каждому лучу одного пучка отвечал определенный луч другого пучка, и обратно. Если при этом оказывается, что ангармоническое отношение четырех лучей всегда равно ангармоническому отношению четырех соответствующих лучей другого пучка, то такое соответствие называется проективным. Проще всего проективное соответствие между двумя пучками устанавливается следующим образом. Рассечем первый пучок O (фиг. 43) прямой, которая дает в сечении с лучами пучка OL (l), ОМ (m), ON (n), ОР (p) точки L, М, N, Р. Теперь каждому из этих лучей отнесем тот луч пучка O′, который пересекает нашу прямую в той же точке. Это значит: лучу ОМ (m) отнесем луч О′М (m′), лучу ON (n) отнесем луч O′N (n′) и т. д. Теперь ясно, что любым четырем лучам p, m, n, l первого пучка отвечают четыре луча p′, m′, n′, l, имеющие то же ангармоническое отношение, ибо ангармоническое отношение как первых, так и вторых четырех лучей равно ангармоническому отношению четырех точек P, М, N, L. Такого рода простейшее проективное соответствие двух пучков называется перспективным. Аналогия с перспективой двух рядов точек совершенно ясна: два ряда точек находятся в перспективном соответствии, если прямые, соединяющие соответственные точки, проходят через одну и ту же точку - центр перспективы. Два пучка находятся в перспективном соответствии, если точки пересечения соответственных лучей лежат на одной прямой - на оси перспективы. Но возможны, конечно, проективные, но не перспективные пучки.

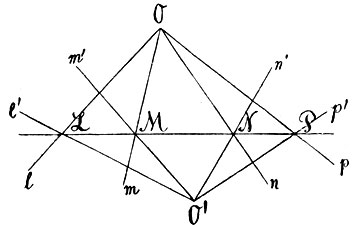
Фиг. 43

Пучки лучей и прямолинейные ряды точек суть простейшие образы проективной геометрии; их называют проективными образами первой ступени. Мы установили понятие о проективном соответствии между двумя рядами точек и между двумя пучками; может быть еще речь о проективном соответствии между пучком и рядом точек; это такое соответствие, при котором 4 лучам пучка отвечают 4 точки с тем же ангармоническим отношением. Если при этом каждый луч пучка проходит через каждую точку ряда, то проективное соответствие обращается в перспективное. Мы уже неоднократно осуществляли перспективное соответствие между пучком и рядом точек; так, на фиг. 41 пучок q, p, m, n, I... перспективен ряду точек Q, P,... L...; с рядом же QP″,... он находится в проективном, но не в перспективном соответствии.

К числу образов первой ступени принадлежит еще пучок плоскостей, проходящих через общую прямую; однако, чтобы не усложнять изложения, мы ограничимся сначала проективным соответствием в плоскости.

Если ангармоническое отношение 4-х точек (PMNL) равно - I, то говорят, что они образуют гармоническую группу или что точки P, М разделяются гармонически точками N, L. Для того, чтобы такое соотношение имело место, два простых отношения, из которых составляется сложное отношение (45), должны быть равны по абсолютной величине и противоположны по знаку, т. е. должно быть

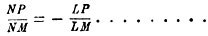
(50)

Это означает, что одна из точек N, L делит расстояние между точками P, М внутренне в том же отношении, в каком другая делит его внешне Если поэтому одна из точек N, L лежит между точками Р, М, то другая лежит вне отрезка. Если точки Р, M, N даны, то построение четвертой точки L так, чтобы удовлетворить соотношению (50), не представляет затруднения. Написав же соотношение (50) в виде:

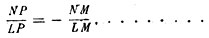
(51)

мы видим, что всякий раз, как точки N и L разделяют гармонически пару точек P, М, эти последние, в свою очередь, разделяют гармонически точки N и L.

Фон-Штаудту принадлежит заслуга сведения проективного соответствия исключительно к свойствам гармонического расположения точек; именно, он доказал следующее предложение: если два непрерывных ряда точек отнесены друг к другу так, Что любым четырем гармоническим точкам одного ряда всегда отвечают четыре гармонические же точки другого ряда, то ангармоническое отношение любых двух точек первого ряда всегда равно ангармоническому отношению соответствующих четырех точек второго ряда. Мы должны только подчеркнуть обстоятельство, недостаточно выдвинутое Штаудтом, что предложение это относится только к непрерывным рядам.

Это важное предложение дало Штаудту возможность определить проективное соответствие след. образ.: два ряда точек связаны проективно, если любым четырем гармоническим точкам одного ряда всегда отвечают четыре гармонические точки другого ряда. Ясно, что таким же образом может быть исключительно при помощи гармонических групп установлено проективное соотношение любых двух образов первой ступени.

Итак, для установления проективного соответствия необходимо предварительно установить только понятие о гармоническом расположении четырех точек или четырех лучей. Но это понятие, как мы видели, устанавливается при помощи метрических соображений: нужно мерить отрезки и определять их отношение. Штаудт, опираясь на теорему Делагира о полном четырехугольнике, освобождает понятие о гармонической группе, а вместе с тем и проективную геометрию от каких бы то ни было метрических соображений.

Пусть MKPQ (фиг. 44) будет обыкновенный четырехугольник, KM, MQ, QP, РК его стороны, РМ и KQ его диагонали. Если мы продолжим противоположные стороны РК и QM, КМ и PQ до пересечения в точках R и S, то получим фигуру, которая носит название полного четырехугольника; точки R и S называются дополнительными вершинами, а прямая RS - дополнительной диагональю. Таким образом получаются 3 диагонали, каждая из которых пересекается двумя другими. Основная теорема, принадлежащая Делагиру, заключается в том, что каждая диагональ полного четырехугольника делится гармонически двумя другими диагоналями; например, диагональ РМ рассекается диагоналями KQ и RS в точках N и L таким образом, что точки P, М разделяются гармонически точками N, L; точно так же точки K, Q разделяются гармонически точками N, T, а точки R, S разделяются гармонически точками L, T, где T есть пересечение диагоналей KQ и RS.

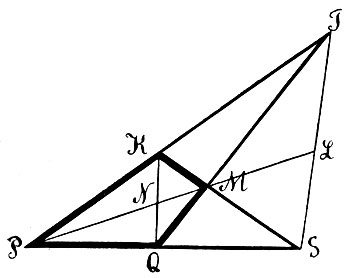
Фиг. 44

Это обстоятельство Штаудт принимает за определение гармонического расположения четырех точек. Иначе говоря, Штаудт определяет гармоническое соответствие следующим образом: четыре точки на одной прямой расположены гармонически, если две из них служат противоположными вершинами полного четырехугольника, а через две другие проходят две его диагонали. Это определение совершенно чуждо каких-либо метрических соображений и освобождает от них всю проективную геометрию. Однако, самое определение требует еще существенного обоснования. В самом деле, это определение фактически устанавливает следующее правило для построения 4-ой гармонической точки. Если нам даны 3 точки P, N, M на одной прямой, то через одну из них, скажем, через Р, проведем произвольно две прямые РК и PQ; через точку N проведем также произвольно третью прямую, пересекающую названные две прямые в точках K и Q; теперь проведем прямые КМ и QM, которые в пересечении с прямыми РК и PQ дадут точки R и S; прямая RS пересечет исходную прямую РМ в точке L, которая и служит четвертой гармонической для исходных 3-х точек; определеннее, точка L вместе с N разделяют гармонически пару точек P, М.

Но при этом построении мы ввели три произвольные прямые: РК, PQ, KQ. Спрашивается, не зависит ли положение точки L от того, как эти 3 прямые выбраны, т. е определяется ли точка L этим построением однозначно. Это очевидно, если гармоническое расположение определяется предварительно метрически и если доказана теорема Делагира; но если мы отрешаемся от предварительного метрического определения и хотим определить точку L исключительно указанным построением, то мы должны доказать однозначность точки L, к которой построение приводит. Это действительно доказывается при помощи теоремы Дезарга, и этим, в первую очередь, определяется коренное значение этой теоремы в проективной геометрии.

Итак, ход идей получается такой. При помощи построения полного четырехугольника устанавливается понятие о четвертой гармонической точке; при помощи теоремы Дезарга устанавливается однозначность этой точки, четыре гармонических луча определяются как такие, которые пересекаются прямою линией в 4 гармонических точках; по сохранению гармонического расположения 4 элементов определяется проективное соответствие образов первой ступени.

Но теорема Дезарга имеет решающее значение еще в одном основном предложении проективной геометрии, которое заключается в следующем: проективное соответствие двух образов первой ступени вполне определено, если указано, какие три элемента одного образа отвечают трем данным элементам другого образа; например, проективное соответствие двух пучков вполне определено, если указано, какие три луча одного пучка соответствуют трем лучам другого пучка. Это предложение по преимуществу принято называть основной теоремой проективной геометрии.

Мы можем теперь перейти к важнейшим приложениям этих идей. Положим, что в одной плоскости расположены два пучка с центрами в точках O и О′. Каждый луч, a, b, c... первого пучка приведем к пересечению с соответствующим лучом а′, d′, с′... второго пучка; получим точки A, В, С... Каково будет геометрическое место этих точек? Если пучки не только проективны, но и перспективны, то эти точки, мы знаем, лежат на прямой линии; но каково геометрическое место этих точек, если наши пучки связаны проективно, но не перспективно? Штейнер первый показал в совершенно общем виде, что это есть коническое сечение и тем положил начало проективному обоснованию учения о кривых 2-го порядка. Мы, таким образом, снова приходим к тем же замечательным кривым; конечно, новый метод не может дать никаких метрических свойств конических сечений; но зато все проективные их свойства раскрываются с необыкновенной простотой и изяществом. Рассмотрим, например, первые шаги в этой теории.

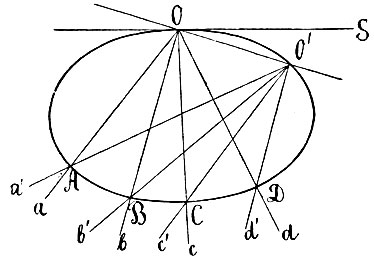
Фиг. 45

Заметим, что вершины двух пучков O и О′ сами принадлежат нашему геометрическому месту, потому что луч OO′ (первого пучка) пересекается с соответствующим ему лучом в точке O′, а луч О′О (второго пучка) пересекается с соответствующим ему лучом первого пучка в точке О. Положим теперь, что нам дано пять точек O, O′, А, В, С, из которых никакие 3 не лежат на одной прямой. Две из этих точек примем за вершины пучков и отнесем лучам OA, OB, OC первого пучка, лучи О′А, О′В, О′С - второго. Этим проективное соответствие двух пучков установлено; следовательно, установлено и геометрическое место точек пересечения соответственных лучей. Таким образом доказывается, что коническое сечение вполне определяется 5 своими точками.

Каждый луч ОА первого пучка пересекается с соответствующим лучом второго в точке А, отличной от O; только луч OS, которому во втором пучке соответствует луч О′O, пересекается с последним только в точке O. Следовательно, прямые, проходящие через точку конического сечения, пересекают его каждая еще в одной точке и только одна из них встречает коническое сечение только в одной точке: иначе говоря, через каждую точку конического сечения проходит одна и только одна касательная к нему; всякая же другая прямая, проходящая через точку конического сечения, встречает его еще в одной, но только в одной точке.

Мы не имеем возможности, конечно, развивать здесь всю проективную теорию конических сечений. Ограничиваясь только выяснением основной идеи, приведем еще одно из замечательнейших предложений, сюда относящихся, - теорему Паскаля: Во всяком шестиугольнике, вписанном в коническое сечение, точки пересечения противоположных сторон лежат на одной прямой.

Однако на учении о полюсах и полярах в проективном изложении мы несколько остановимся. Пусть O будет произвольная точка в плоскости конического сечения, но ему не принадлежащая. Проведем через эту точку произвольную прямую, встречающую коническое сечение в точках K и L. Пусть М будет точка, которая вместе с O делит гармонически отрезок KL. Если прямая вращается вокруг точки O, то вместе с этим перемещается точка М и описывает, как оказывается, прямую линию. Эта прямая и называется полярой точки O относительно конического сечения. Если точка O лежит вне конического сечения, то точка М лежит между K и L. Если поэтому секущая вращается таким образом, что точки K и L сближаются между собой, то к ним приближается и расположенная между ними точка M. Когда обе точки сливаются в одну, то с ними сливается и точка М, иными словами, когда секущая обращается в касательную, то поляра проходит через точку касания. Это возвращает нас к прежнему определению поляры.

С учением о полюсах и полярах находится в тесной связи очень важная в проективной геометрии идея - начало двойственности; оно заключается в следующем. Проективная геометрия разматывается из известных положений, касающихся расположения и инцидентности основных образов. Возьмем следующие два из этих положений: каждые две точки определяют проходящую через них прямую, каждые две прямые определяют точку, через которую они обе проходят (как мы сказали выше, последнее положение не имеет исключений в проективной геометрии). Мы формулируем теперь эти предложения немножко иначе, пользуясь терминологией, которую мы уже указали в отделе I (рубрика 3). Точка и прямая называются инцидентными, если прямая проходит через точку или точка лежит на прямой. При таких условиях предыдущие два положения можно формулировать так: каждые две точки определяют инцидентную с ними прямую; каждые две прямые определяют инцидентную с ними точку. Эти два положения таковы, что одно переходит в другое, если мы заменим друг другом термины "прямая" и "точка". Замечательно, что таковы все положения, из которых разматывается проективная геометрия; они переходят одно в другое, если заменить эти термины "точка" и "прямая" друг другом. Вследствие этого каждая теорема проективной геометрии переходит в новую теорему, если термины "точка" и "прямая" заменить друг другом. Именно, в соотношении двойственности находятся полюс и поляра друг к другу. При замене понятий "точка" и "прямая" друг другом свойства полюса обращаются в свойства поляры, и обратно.

Выше мы выяснили, как образуется кривая второго порядка при помощи двух проективных пучков лучей. Постараемся выяснить, как можно преобразовать эту теорию по принципу двойственности. Два пучка прямых заменим двумя рядами точек. Если эти ряды расположены перспективно, то прямые, соединяющие соответственные точки, проходят через общую точку - центр перспективы. Но если эти ряды связаны проективно, но не перспективно, то прямые, соединяющие соответственные точки, не пересекаются в одной точке, а огибают некоторую кривую (фиг. 46). Эта кривая оказывается коническим сечением.

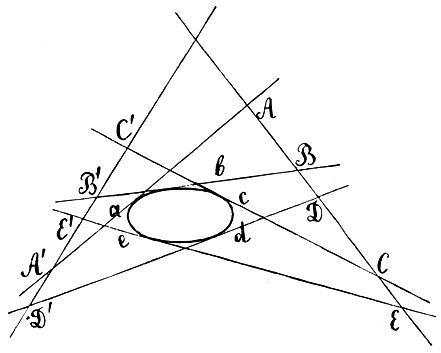
Фиг. 46

Коническое сечение может быть рассматриваемо, как геометрическое место точек пересечения соответственных лучей двух проективных пучков или как огибающая прямых, соединяющих соответственные точки двух проективных рядов. Таковы две точки зрения, связанные принципом двойственности. Теорема Паскаля по принципу двойственности переходить в теорему Брианшона: во всяком шестиугольнике, описанном около конического сечения, прямые, соединяющие попарно противоположные вершины, проходят через одну точку.

Мы с достаточной подробностью выяснили основные моменты в учении о проективном соответствии образов первой ступени и ограничимся лишь самыми краткими указаниями относительно проективного соответствия более сложных образов.

Образами второй ступени являются плоскость, как совокупность точек, плоскость, как совокупность прямых; связка прямых, т. е. совокупность прямых в пространстве, проходящих через одну точку; связка плоскостей, т. е. совокупность плоскостей, проходящих через общую точку. В рубрике 4 отд. 1-го было выяснено, как устанавливается перспективное соответствие между точками двух плоскостей. Проективное соответствие между точками двух плоскостей определяется тем, что четырем гармоническим точкам одной плоскости всегда отвечают четыре гармонические точки другой плоскости. На том же принципе основано определение проективного соответствия других образов высших ступеней.

Чрезвычайно любопытно, что всякое геометрическое соответствие в плоскости или в пространстве, при котором прямой линии всегда соответствует прямая же линия, представляет собою проективное соответствие. С этой точки зрения проективное соответствие часто называют еще коллинеацией.

Подобно тому, как при помощи проективных пучков определяется кривая второго порядка, при помощи проективных связок определяются поверхности второго порядка. Но, мало того, в том же порядке идей могут быть даны методы построения алгебраических кривых более высоких порядков. Это обобщение может идти различными путями: путем установления более сложных проективных рядов и путем перенесения идеи проективного соответствия на более сложные образы, например, на пучки конических сечений. Относящиеся сюда исследования носят уже слишком специальный характер и не могут найти места в настоящем изложении. Изложенное выше, полагаем, достаточно выясняет, что наряду с аналитической геометрией выросли новые строго геометрические методы исследования, глубоко отличающиеся от приемов классической геометрии и дающие чистому геометру орудие для соревнования с аналистом; и насколько сильно это орудие, можно судить по тому, что сведения, которыми мы обладаем относительно метрики высших алгебраических кривых, незначительны по сравнению с известными нам проективными свойствами их.

Нужно к этому прибавить, что в последние два десятилетия во Франции получило развитие новое учение, занимающее как бы среднее место между проективной и метрической геометрией. Лемуан (Lemoine), Брокар (Broccard), Лезан (Laisant), Нейберг (Neuberg) и др. развили учение об особенных точках треугольников и многоугольников в целую новую дисциплину, которая по своим методам особенно приближается к классической геометрии. Эта дисциплина получила название "новой геометрии треугольника". Результаты этих методов отличаются необычайным изяществом, но они носят характер как бы случайных, более остроумных, нежели глубоких открытий. Какого-либо общего метода геометрического исследования эти идеи с собою не принесли.

IX. Геометрография.

Уже в античную эпоху греческих геометров чрезвычайно занимали так называемые задачи на построение. Мы уже указывали (см. в тексте) сочинения греческих геометров, посвященные исключительно задачам на построение; в "Началах" Евклида эти задачи чередуются с предложениями, и решение их имеет цельно, главным образом, доказать существование определенных образов. На эти задачи можно смотреть с двух точек зрения. Более теоретическая точка зрения заключается в том, что одними геометрическими элементами определяются другие, и задача заключается в том, чтобы это обнаружить. Так, например, треугольник определяется тремя своими сторонами, двумя сторонами и углом между ними, стороной и двумя углами и т. д. Яркое выражение эта точка зрения получила в "Данных" Евклида. Другая, более техническая точка зрения заключается в том, чтобы по определенным графически заданным элементам образа графически же воспроизвести другие части этого образа. Это графическое воспроизведение носит название черчения; в этой постановке решение задачи на построение имеет две стадии: геометрическую подготовку, указание тех построений, которые должны быть выполнены, и осуществление этих построений; первая стадия составляет предмет геометрографии, вторая - черчения (см.).

Но раз геометр должен подготовлять указания, которыми воспользуется чертежник, он должен знать, какими инструментами, какими орудиями последний располагает. И подобно тому, как скульптор может дать более или менее тонкую работу в зависимости от инструментов, которыми он располагает, и геометр может справиться с более или менее трудной задачей в зависимости от инструментов, которые предоставлены в его распоряжение. Классическая геометрия признавала только два таких инструмента: линейку и циркуль; с точки зрения теоретической это значит, что геометру предоставлялось оперировать только прямыми линиями и окружностями; их пересечением должны определяться искомые точки.

Геометрия знает фактически только два метода решения задач на построение. Первый из них называется методом геометрических мест и заключается в следующем. Решение задачи сводят к определению одной или нескольких точек. Каждая из этих точек определяется рядом условий. Если мы оставим одно из этих условий, то остальным будет удовлетворять бесчисленное множество точек; разыскивается их геометрическое место. Затем мы восстанавливаем опущенное условие и вместо него опускаем другое; теперь точки, удовлетворяющие нашим условиям, образуют другое геометрическое место; в пересечении этих двух геометрических мест лежат искомые точки. Положим, например, что нам нужно построить треугольник по основанию, углу при вершине и соответствующей высоте. Если возьмем отрезок, равный основанию, то задача сводится к разысканию вершины треугольника. Если теперь оставим в стороне второе задание (высоту), то геометрическое место вершин треугольников с данным основанием и данным углом при вершине будет дуга окружности. Если же оставим первое условие, а будем иметь в виду только данную высоту, то геометрическое место вершин будет прямая линия. В пересечении этой дуги и прямой и лежит вершина искомого треугольника.

Второй метод заключается в том, что в плоскости или в пространстве устанавливается некоторое геометрическое соответствие и вместо искомой фигуры строится предварительно преобразованная фигура, по которой уже обратным преобразованием восстанавливается искомая фигура. Этот метод имеет много разновидностей, смотря по характеру устанавливаемого соответствия: иногда строится фигура, конгруэнтная данной, но в ином положении, или фигура, подобная данной, или перспективная, или проективная, или двойственная данной и т. д.

Греки были большие мастера в деле решения задач на построение. Однако, уже у них составилась группа задач, справиться с которыми они не были в состоянии. Три задачи этого рода особенно замечательны: задача об удвоении куба (Делийская задача), т. е. о построении по данной стороне куба стороны такого куба, который имеет вдвое больший объем; задачи о трисекции угла (т. е. о разделении любого угла на 3 равные части) и о квадратуре круга, т. е. о построении квадрата, равновеликого данному кругу. Эти задачи представляли настоящие камни преткновения человеческой мысли; трудно себе представить, сколько бесплодных усилий было затрачено на их разрешение. Полное выяснение этого вопроса принадлежит, однако, уже только XIX столетию. Геометры не принимали во внимание, что они требуют построений определенными средствами - циркулем и линейкой - и что этих средств может оказаться для выполнения требуемого построения недостаточно. Лишь аналитическая геометрия была в состоянии дать ответ на вопрос, какие задачи могут быть решены циркулем и линейкой, какие ее могут быть решены. Ответ этот сводится к следующему. Всякая задача может быть приведена к построению одного или нескольких отрезков; если, например, требуется построить некоторую точку, то это может быть приведено к построению ее декартовых координат. Длины этих отрезков могут быть выражены алгебраически в зависимости от заданий. Циркулем и линейкой могут быть построены только такие отрезки, которые выражаются в зависимости от данных рационально или при помощи квадратных корней. Такие же отрезки, которые выражаются более сложными алгебраическими формами, не разрешающимися в ряд рациональных и квадрато-радикальных операций, построены быть не могут. Ванцель (L. Wantzell, 1837) впервые доказал, что задача о трисекции угла зависит от уравнения 3-ей степени, которое никоим образом не может быть разрешено при помощи ряда квадратных корней. Этим было обнаружено, что задача о трисекции угла не разрешается циркулем и линейкой; задача об удвоении куба исчерпывается теми же средствами. Гораздо сложнее было обнаружить невозможность квадратуры круга (см. квадратура). Здесь заметим только, что это было впервые строго доказано Линдеманом (F. Lindemann) только в 1882 г. Эти исследования имели чрезвычайно важное значение, так как они положили начало целому ряду изысканий относительно возможности выполнения тех или иных алгебраических и геометрических операций заданными средствами.

В тесной связи с этим находится теоретически вопрос о том, какие задачи решаются более ограниченными еще средствами, чем те, которыми пользуется классическая геометрия, - например - одной линейкой, одной окружностью. Совершенно ясно, что одной линейкой решаются проективные задачи. Маскерони (Mascheroni, 1797) показал, что при помощи одного циркуля можно решать все задачи, какие решаются циркулем и линейкой. Штейнер же обнаружил, что те же задачи могут быть также решены одной линейкой, если в плоскости дана одна окружность.

В самые последние годы, главным образом, Лемуан (Lemoine, 1902, предварительные работы 1888-1893 гг.) поставил вопрос о простейшем решении данной конструктивной задачи; эти именно исследования в настоящее время по преимуществу называют "геометрографией", а решение, удовлетворяющее требованию наибольшей простоты, называют геометрографическим. Для математической оценки простоты решения все конструктивные приемы разбиваются на ряд элементарных операции, и то построение признается наиболее простым, которое требует наименьшего числа этих элементарных приемов. Задача геометрографии заключается в указании для каждой задачи того построения, которое удовлетворяет этим требованиям наибольшей простоты. Нужно, однако, сказать, что в установлении элементарных операций остается достаточно места произволу. С другой стороны, многие справедливо находят, что простота и изящество геометрического построения не могут быть оцениваемы сухим перечислением элементарных операций. Все направление имеет поэтому решительных противников.

X. Начертательная геометрия.

В предыдущем отделе, быть может, недостаточно подчеркнуто, что все построения, о которых идет речь, выполняются в плоскости. Хотя линейка определяет прямую линию независимо от плоскости, но циркуль чертит окружность только в плоскости. Да и вообще черчение, как и всякое графическое изображение, возможно только на некоторой поверхности, лучше и проще всего - на плоскости. Воспроизведение геометрических образов в пространстве падает уже в область пластики. Между тем множество геометрических задач на построение в пространстве представляет для геометрии не меньший интерес, а по своей трудности - и больший. Отсюда естественное стремление перенести на плоскость те построения, которые, собственно, должны быть выполнены в пространстве. Но та же задача возникает с гораздо большею настойчивостью на другой почве. Изобразить на плоскости образы трехмерного пространства является насущной необходимостью не только в области техники, но и во многих отраслях культурной деятельности человека. Это достигалось рисованием, искусством столь же древним, как и геометрия. Но искусство рельефного воспроизведения образов в течение веков оставалось достоянием особого дарования, чуждое общих правил в научной теории. Поскольку речь идет о воспроизведении наружного сходства, об изображении, которое оказывало бы воздействие на глаз всякого непосвященного, словом, о художественном воспроизведении, таковое и по настоящее время относится к области искусства, и геометрическая теория играет здесь лишь весьма второстепенную роль. Но если речь идет о таком графическом воспроизведении пространственных образов на плоскости, которое давало бы возможность с точностью восстановить геометрические размеры и расположение изображаемого объекта, то здесь уже нет места свободному художеству; на место его выступает строгая общая теория - начертательная геометрия.

Основной метод, проникающий все разнообразные приемы начертательной геометрии, есть центральное проектирование. Это метод, можно сказать, и естественный, ибо наш глаз постоянно проектирует на ту или иную плоскость созерцаемые объекты. Рельефное (стереоскопическое) падение, как известно, заключается в сведении двух центральных проекций. Расположение теней также определяется центральной проекцией освещенных и неосвещенных частей объекта.

Вопрос о теоретическом обосновании рельефного изображения имеет древнее происхождение; в архитектуре и живописи он, естественно, возник еще в пору первого сознательного отношения к этому делу. Попытки теоретического обоснования архитектурного черчения мы находим уже у римского архитектора Витрувия (Marcus Vitruvius Pollio, "De architectura"), III в.). К этому возвращаются многие живописцы и архитекторы эпохи возрождения с Леонардо да Винчи во главе. Знаменитый художник Альберт Дюрер (A. Durer, XV, XVI ст.) первый сделал попытку дать общую теорию геометрического черчения. Дюрера нередко называли отцом начертательной геометрии. Дюрер прежде всего художник; геометрические формы интересуют его лишь постольку, поскольку он понимал, что их нельзя обойти в теории перспективы. Отцом или, вернее, дедом начертательной геометрии нужно считать Дезарга, о котором мы уже говорили в отделе VIII. Разрозненные по содержанию, но единые по духу идеи Дезарга о перспективе, о трансверсалях, о конических сечениях, о полюсах и полярах, как мы видели, послужили началом новой синтетической геометрии. Понсле и Шаль использовали эти идеи и положили их в основу теоретической дисциплины - проективной геометрии; Монж создал, исходя из тех же идей, прикладную науку - начертательную геометрию.

Основная идея Монжа заключается в следующем. При помощи одной проекции можно получить лишь перспективное изображение фигуры, дающее общее представление о ее форме и расположение частей. Воспроизвести размеры фигуры в точности по одной проекции невозможно. Это особенно ясно уже потому, что все точки, лежащие на одном и том же проектирующем луче, проектируются в одну и ту же точку плоскости изображения (картинная плоскость). Для того, чтобы по изображению действительно можно было точно воспроизвести геометрическую форму и положение объекта, нужна не одна, а две проекции на две различные плоскости. Между тем изображение требуется воспроизвести в одной плоскости. Монж выходит из этого затруднения след. образом.

Пусть Р и Q будут две взаимно перпендикулярные плоскости, скажем, первая горизонтальная, вторая вертикальная. Пусть М (фиг. 47) будет произвольная точка в пространстве. Опустим из нее перпендикуляры на плоскости, т. е спроектируем ее на обе плоскости в точки m и m′. Ясно, что две проекции m и m′ не только вполне определяются точкой M, но и, обратно, определяют положение последней в том смысле, что по этим двум проекциям не трудно воспроизвести точку М. Если, таким образом, нам дана горизонтальная и вертикальная проекция всех точек некоторой фигуры, то мы сможем воспроизвести и всю фигуру. Так, на фигуре 47 mn и m′n′ суть проекции прямой MN, которую легко по этим проекциям воспроизвести. Задача была бы разрешена, если бы изображение не распадалось на две части, расположенные на двух взаимно перпендикулярных плоскостях. Остается сделать еще один шаг: свести обе проекции в одну плоскость. Монж поворачивает для этого плоскость Q на 90° в направлении, указанном стрелкой, так что плоскость Q падает на плоскость Р. Два изображения, сведенные таким образом в одну плоскость, имеют вид, изображенный на фигуре 48. Изображение, составленное из двух проекции, которые сведены в одну плоскость, называется эпюром. Совершенно ясно, что по эпюру мы имеем возможность восстановить вполне изображаемый объект. Каждая точка пространства М однозначно изображается, таким образом, двумя точками m и m на эпюре. Значок на букве отличает вертикальную проекцию от горизонтальной, а по этим проекциям, как уже выяснено, мы можем восстановить точку М.

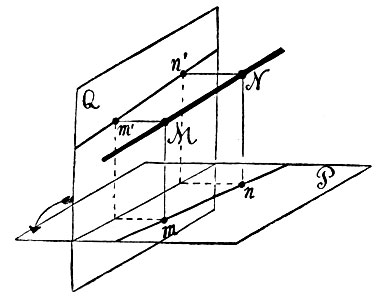
Фиг. 47

Фиг. 48

Этим, по существу, основная идея Монжа исчерпывается. Но если нам нужно воспроизвести объект, то по этому правилу пришлось бы разыскивать две проекции каждой точки и по этим проекциям наносить ее на эпюр. Это представляет, конечно, непреодолимые затруднения; да к тому же проекции сплошных образов заполняли бы целые участки чертежа и налагались бы друг на друга. Но задача упрощается тем, что чаще всего приходится чертить эпюр тела или поверхности, имеющего определенные геометрические формы. На чертеж наносятся контуры, определяющие форму тела; но самые эти контуры определяются обыкновенно небольшим числом элементов; задача теории заключается в том, чтобы указать методы построения геометрических образов по определяющим их элементам. Например, положение и размеры куба вполне определяются, если даны два смежных ребра; нужно, следовательно, показать, как построить эпюр куба, когда нанесены проекции двух его смежных ребер.

Прямая определяется двумя своими точками, плоскость - тремя точками; по этим элементам нужно уметь воспроизвести т. н. "следы" прямой, т. е. точки ее пересечения с плоскостями проекций, и "следы" плоскости, т. е. прямые, по которым она пересекает плоскости проекции. Нужно уметь разыскать пересечение прямой с плоскость, пересечение плоскостей, определять, пересекаются ли нанесенные на эпюр прямые и т. д. Решение всех этих задач в составляет содержание начертательной геометрии. Идеи Монжа разработаны его учениками, главным образом, Гашетом (Hachette) и Брисоном (Brisson). Методы для простейшего изображения геометрических образов очень детально разработаны. Основная идея всех этих методов заключается в следующем: если нужно изобразить какую-либо геометрическую фигуру в определенном положении, то сначала ставят ее в положение, наиболее благоприятное для проектирования; затем переводят из этого положения в требуемое. Сообразно этому существенно важной задачей в начертательной геометрии является преобразование эпюра сообразно перемещению объекта или изменению плоскостей проекций.

Кроме метода "свободной проекции", ведущего свое происхождение от Монжа, в настоящее время часто применяется так называемая осевая или аксонометрическая проекция. Здесь идея заключается в следующем. Изображаемое геометрическое тело относят к некоторой системе декартовых координат; координаты каждой точки выражаются, следовательно, тремя отрезками. Затем оси координат и эти отрезки проектируются па плоскость изображения. По проекциям координат восстанавливаются самые координаты, а по ним изображаемая точка. Мы лишены возможности входить здесь в большие подробности относительно этого метода.

Нам остается еще указать теоретическое значение начертательной геометрии. Как было выяснено выше, эпюр содержит в плоскости все расположение пространственных образов. Каждому соотношению проективному и метрическому пространственных объектов отвечает некоторое соотношение между соответствующими элементами на эпюре и обратно. Отсюда следует, что изучение эпюра эквивалентно изучению пространственных соотношений и начертательная геометрия содержит средства для планиметрического исследования стереометрических соотношений. Эти методы оказались весьма плодотворными в деле исследования многогранников, кривых пересечения алгебраических поверхностей, линейчатых поверхностей и т. д.

XI. Неевклидова геометрия.

Изложенный выше материал содержит весьма краткий очерк современного фактического развития геометрии. Но кроме вопросов строго фактического свойства, геометрия проникнута целым рядом глубоких философских вопросов. Геометрия разматывается из небольшого числа основных положений - ее определений и аксиом. Каковы эти аксиомы? Каков их источник? Как убедиться в том, что те или иные положения не могут быть данными средствами доказаны и должны быть приняты за аксиомы? В чем заключается независимость аксиом и как она устанавливается? Каковы наиболее простые основные понятия, к которым должно быть сведено все остальное? Вот вопросы, которые издавна одинаково интересовали геометров и философов. Относящаяся сюда литература необычайно велика, и от Платона до Канта можно с трудом назвать философа, который не старался бы внести свет в эти темные вопросы. Однако, лишь последнее столетие принесло с собой значительное выяснение этих вопросов. Но путь, приведший к современным взглядам на начало основы математики лежит через математику, а не через философию. В арифметике и в геометрии возникли совершенно новые теории, новые дисциплины, которым собственно мы и обязаны выяснением этих вопросов. Эти новые дисциплины в геометрии известны в настоящее время под общим названием "неевклидовой геометрии". Все вопросы философского характера, относящиеся к арифметике, анализу и геометрии, сконцентрированы в особой статье Основания математики. Там найдет себе место и "неевклидова геометрия".

Библиография.

Литература геометрии чрезвычайно велика. По каждому отделу под рубрикой α) указаны важнейшие классические сочинения, трактаты; под рубрикойβ) сочинения, более доступные для широкого круга читателей.

По истории геометрии. α) M. Cantor, "Geschichte der Mathematik"; W. Rouse Ball, "A schortc account of the history of mathematics" (имеется французский перевод W. Rouse Ball, "Histoire des mathématiques"). P. Tannery, "La géométrie grecque"; М. Ващенко-Захарченко, "История геометрии". β) Tropfke, "Geschichte der Elementarmathematik"; Ф. Кэджори, "История элементарной математики".

I. α) Лучший трактат по элементарной геометрии: E. Rouché et Ch. de Comberousse, "Traité de géométrie I, II. β) Наиболее распространенные у нас руководства по элементарной геометрии гг. Киселева, Давыдова, Симашко заслуженно пользуются значительным распространением. Ващенко-Захарченко, "Элементарная геометрия". Более научное изложение важнейших вопросов элементарной геометрии можно найти в сочинении Вебер и Велльштейн, "Энциклопедия элементарной Математики" т. II (перевод с немецкого).

Из сочинений, касающихся отдельных вопросов элементарной геометрии, особенного внимания заслуживают: Ф. Клейн, "Сравнительное обозрение новейших геометрических исследований" (перевод с немецкого); F. Enriques, "Fragen der Elementargeometrie" (приводим немецкий перевод вместо итальянского оригинала).

Издания Евклида: α) Heiberg und Menge, "Euclidis opera omnia" (греч. и латинский текст); Heath, "The thirteen books of Euclid'e Elements". Английский перевод с многочисленными примечаниями; лучшее справочное издание. Ващенко-Захарченко, "Начала Евклида". β) M. Simon, "Euclid und die sechs planimetrischen Bücher".

II. О конических сечениях. α) M. Chasles, "Traité des sections coniques"; A. Clebsch, "Vorlesungen über Geometrie". Bd. I; O. Hesse, "Sieben Vorlesungen aus der analytischen Geometrie der Kegelschnitte"; β) H. Zeuthen, "Grundriss einer elementar-geometr. Kegelschinittslehre". J. Schlotke, "Die Kegelschnitte und ihre wichtigsten Eigenschaten in elementar-geometrischer Behandlung" Из различных изданий Аполлония наиболее подходящим является английское издание Heath, "Apollonius of Perga, Treatise of conic sections".

III-V. Аналитическая геометрия. α) B. Niewenglowski, "Cours de géométrie analytique". I-III. Salmon, "Analytische Geometrie der Kegelschnitte", "An. G. der höheren ebenen Kurven". "An. Geometrie des Raumes" frei bearbeitet von Fiedler. Приводим немецкую обработку, так как она превосходит английский оригинал. β) Briot et Bouquet "Leçons des géométrie analytique"; J. Neuberg, "Cours de géométrie analytique"; К. Андреев, "Курс аналитической геометрии"; Б. Млодзееевский, "Аналитическая геометрия на плоскости"; Дзиабек, "Курс аналитической геометрии".

VI-VII. Дифференциальная геометрия изложена во всех курсах анализа (см. исчисление бесконечно малых), но имеются и специальные сочинения: α) L. Bianchi, "Vorlesungen über Differentialgeometrie (приводим немецк. перевод вместо итальянского оригинала). L. Raffy, "Leçons sur les applications géométriques de I'analyse". β) F. Joachimsthal, "Anwendung der Differential und integralrechnung auf die allgemeine Theorie der Flächen und der Linien doppelter Krümmung". Б. Я. Букреев. "Курс приложений дифференциального и интегрального исчисления к геометрии.

VIII. Проективная геометрия. α) M. Chasles, "Traitée de géométrie supérieure". J. Steiner, "Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von einander". Th. Reye, "Die Geometrie der Lage. β) F. Enriques, "Vorlesungen uber projective Geometrie", autorisierte deutsche Ausgabe von H. Fleischer R. Böger, "Ebene Geometrie der Lage"

IX. Геометрография. α) Th. Vahlen, "Konstruktionen und Approximationen in systematischer Darstellung". β) И. Александров, "Методы решений геометрических задач на построение". Weber u. Wellstein, "Encyklopädie der Elementar-Mathematik", Band III, отд. V. Graphik (этот том по-русски еще не издан); А. Адлер, "Теория геометрических построений".

X. Начертательная геометрия. α) G. Monge "Leçons de géométrie descriptive". S. F. Lacroix, "Essai de géométrie sur les plans et les surfaces courbes". K. Poh'ke. "Darstellende Geometrie". β) F. Smolik. "Elemente der darstellenden Geometrie". Н. Макаров. "Начертательная геометрия". И. Сомов. "Начертательная геометрия". А. Польшау. "Начала начертательной геометрии, теории теней и линейной перспективы".

В. Каган.

Источники:

1. Энциклопедический словарь Русского библиографического института Гранат. Том 13/13-е стереотипное издание, до 33-го тома под редакцией проф. Ю. С. Гамбурова, проф. В. Я. Железнова, проф. М. М. Ковалевского, проф. С. А. Муромцева и проф. К. А. Тимирязева- Москва: Русский Библиографический Институт Гранат - 1937.